
【題目】有一個拋物線型蔬菜大棚,將其截面放在如圖所示的平面直角坐標系中,拋物線可以用函數y=ax2+bx來表示.已知大棚在地面上的寬度OA為8米,距離O點2米處的棚高BC為![]() 米.
米.
(1)求該拋物線的函數關系式;
(2)若借助橫梁DE建一個門,要求門的高度不低于1.5米,則橫梁DE的寬度最多是多少米?

科目:初中數學 來源: 題型:
【題目】如圖,已△ABC中,AB=AC=12厘米(可得出∠B=∠C),BC=9厘米,點D為AB的中點.如果點P在線段BC上以3厘米/秒的速度由B向C點運動,同時點Q在線段CA上由C點向A點運動.

(1)若點Q的運動速度與點P的運動速度相等,1秒鐘時,△BPD與△CQP是否全等,請說明;
(2)點Q的運動速度與點P的運動速度不相等,當點Q的運動速度為多少時,能夠使△BPD≌△CPQ?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,Rt△ABC中,若AC=4,BC=3,DE⊥AC,且DE=DB,求AD的長;
(2)如圖2,已知△ABC,若AB邊上存在一點M,若AC邊上存在一點N,使MB=MN,且△AMN∽△ABC,請利用沒有刻度的直尺和圓規,作出符合條件的線段MN(注:不寫作法,保留作圖痕跡,對圖中涉及到的點用字母進行標注).
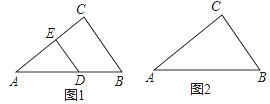
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() (a>0)圖象的頂點為D,其圖象與x軸的交點A、B的橫坐標分別為﹣1和3,則下列結論正確的是( )
(a>0)圖象的頂點為D,其圖象與x軸的交點A、B的橫坐標分別為﹣1和3,則下列結論正確的是( )

A. 2a﹣b=0
B. a+b+c>0
C. 3a﹣c=0
D. 當a=![]() 時,△ABD是等腰直角三角形
時,△ABD是等腰直角三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,解答問題
(2x﹣5)2+(3x+7)2=(5x+2)2
解:設m=2x﹣5,n=3x+7,則m+n=5x+2
則原方程可化為m2+n2=(m+n)2
所以mn=0,即(2x﹣5)(3x+7)=0
解之得,x1=![]() ,x2=﹣
,x2=﹣![]()
請利用上述方法解方程(4x﹣5)2+(3x﹣2)2=(x﹣3)2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市創建“綠色發展模范城市”,針對境內長江段兩種主要污染源:生活污水和沿江工廠污染物排放,分別用“生活污水集中處理”(下稱甲方案)和“沿江工廠轉型升級”(下稱乙方案)進行治理,若江水污染指數記為Q,沿江工廠用乙方案進行一次性治理(當年完工),從當年開始,所治理的每家工廠一年降低的Q值都以平均值n計算.第一年有40家工廠用乙方案治理,共使Q值降低了12.經過三年治理,境內長江水質明顯改善.
(1)求n的值;
(2)從第二年起,每年用乙方案新治理的工廠數量比上一年都增加相同的百分數m,三年來用乙方案治理的工廠數量共190家,求m的值,并計算第二年用乙方案新治理的工廠數量;
(3)該市生活污水用甲方案治理,從第二年起,每年因此降低的Q值比上一年都增加個相同的數值a.在(2)的情況下,第二年,用乙方案所治理的工廠合計降低的Q值與當年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC為直角三角形,∠C=90°,BC=2cm,∠A=30°,四邊形DEFG為矩形,DE=2![]() cm,EF=6cm,且點C、B、E、F在同一條直線上,點B與點E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的邊EF向右平移,當點C與點F重合時停止.設Rt△ABC與矩形DEFG的重疊部分的面積為ycm2,運動時間xs.能反映ycm2與xs之間函數關系的大致圖象是( )
cm,EF=6cm,且點C、B、E、F在同一條直線上,點B與點E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的邊EF向右平移,當點C與點F重合時停止.設Rt△ABC與矩形DEFG的重疊部分的面積為ycm2,運動時間xs.能反映ycm2與xs之間函數關系的大致圖象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二維碼已經給我們的生活帶來了很大方便,它是由大小相同的黑白兩色的小正方形(如圖1中C)按某種規律組成的一個大正方形,現有25×25格式的正方形如圖1,角上是三個7×7的A型大黑白相間正方形,中間右下一個5×5的B型黑白相間正方形,除這4個正方形外,若其他的小正方形白色塊數y與黑色塊數x正好滿足如圖2所示的函數圖象,則該25×25格式的二維碼共有多少塊黑色的C型小正方形( )

A. 153 B. 218 C. 100 D. 216
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com