
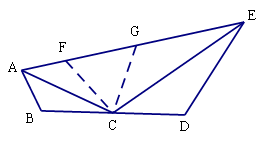
在四邊形ABDE中,C是BD邊的中點.
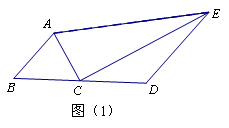
(1)如圖(1),若AC平分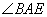 ,
,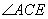 =90°, 則線段AE、AB、DE的長度滿足的數量關系為
=90°, 則線段AE、AB、DE的長度滿足的數量關系為
;(直接寫出答案)
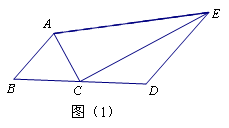
(2)如圖(2),AC平分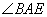 , EC平分
, EC平分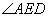 ,
,
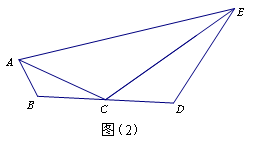
若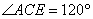 ,則線段AB、BD、DE、AE的長度滿足怎樣的數量關系?寫出結論并證明;
,則線段AB、BD、DE、AE的長度滿足怎樣的數量關系?寫出結論并證明;

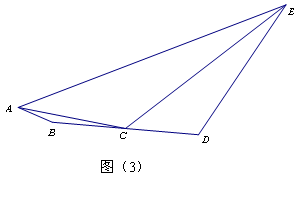
(3)如圖(3),BD = 8,AB=2,DE=8,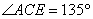 ,則線段AE長度的最大值是____________(直接寫出答案).
,則線段AE長度的最大值是____________(直接寫出答案).

(1) AE=AB+DE ;
 (2)解:猜想:AE=AB+DE+
(2)解:猜想:AE=AB+DE+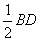 .
.
證明:在AE上取點F,使AF=AB,連結CF,
在AE上取點G,使EG=ED,連結CG.
∵C是BD邊的中點,∴CB=CD=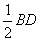 .
.
∵AC平分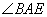 ,∴∠BAC=∠FAC.
,∴∠BAC=∠FAC.
∵AF=AB,AC=AC,∴△ABC≌△AFC.
∴CF=CB,∴∠BCA=∠FCA.同理可證:CD=CG,∴∠DCE=∠GCE.
∵CB=CD,∴CG=CF
∵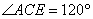 ,∴∠BCA+∠DCE=180°-120°=60°. 圖(2)
,∴∠BCA+∠DCE=180°-120°=60°. 圖(2)
∴∠FCA+∠GCE=60°.∴∠FCG=60°.
∴△FGC是等邊三角形.∴FG=FC=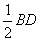 .
.
∵AE=AF+EG+FG.
∴AE=AB+DE+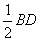 .(3)
.(3) .
.



科目:初中數學 來源: 題型:
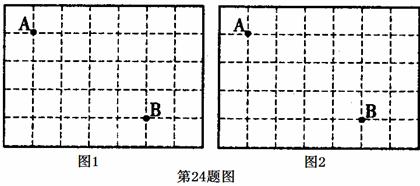
圖l、圖2是兩張形狀、大小完全相同的方格紙,方格紙中的每個小正方形的邊長均為1.點A和
點B在小正方形的頂點上.
(1) 在圖1中畫出△ABC(點C在小正方形的頂點上),使△ABC為直角三角形
(畫一個 即可);
(2) 在圖2中畫出△ABD(點D在小正方形的頂點上),使△ABD為等腰三角形
(畫一個即可);
查看答案和解析>>
科目:初中數學 來源: 題型:
陳老師打算購買氣球裝扮學校“六一”兒童節活動會場,氣球的種類有笑臉和愛心兩種,兩種氣球的價格不同,但同一種氣球的價格相同,由于會場布置需要,購買時以一束(4個氣球)為單位,已知第一、二束氣球的價格如圖所示,則第三束氣球的價格為( )元.
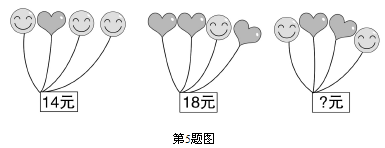
A.19 B.18 C.16 D.15
查看答案和解析>>
科目:初中數學 來源: 題型:
下面關于公理和定理的說法不正確的是( )
A.公理和定理都是真命題
B.公理就是定理,定理也是公理
C.公理和定理都可以作為推理論證的依據
D.公理的正確性不需證明,定理的正確性需證明
查看答案和解析>>
科目:初中數學 來源: 題型:
計算(-8m4n+12m3n2-4m2n3)÷(-4m2n)的結果等于( )
A.2m2n-3mn+n2 B.2n2-3mn2+n2
C.2m2-3mn+n2 D.2m2-3mn+n
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com