
【題目】如圖,已知在△ABC中,AB=15,AC=20,tanA=![]() ,點(diǎn)P在AB邊上,⊙P的半徑為定長(zhǎng).當(dāng)點(diǎn)P與點(diǎn)B重合時(shí),⊙P恰好與AC邊相切;當(dāng)點(diǎn)P與點(diǎn)B不重合時(shí),⊙P與AC邊相交于點(diǎn)M和點(diǎn)N.
,點(diǎn)P在AB邊上,⊙P的半徑為定長(zhǎng).當(dāng)點(diǎn)P與點(diǎn)B重合時(shí),⊙P恰好與AC邊相切;當(dāng)點(diǎn)P與點(diǎn)B不重合時(shí),⊙P與AC邊相交于點(diǎn)M和點(diǎn)N.
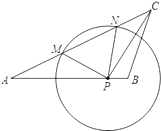
(1)求⊙P的半徑;
(2)當(dāng)AP=![]() 時(shí),試探究△APM與△PCN是否相似,并說(shuō)明理由.
時(shí),試探究△APM與△PCN是否相似,并說(shuō)明理由.
【答案】(1)半徑為3![]() ;(2)相似,理由見(jiàn)解析.
;(2)相似,理由見(jiàn)解析.
【解析】(1)如圖,作BD⊥AC,垂足為點(diǎn)D,⊙P與邊AC相切,則BD就是⊙P的半徑,利用解直角三角形得出BD與AD的關(guān)系,再利用勾股定理可求得BD的長(zhǎng);
(2)如圖,過(guò)點(diǎn)P作PH⊥AC于點(diǎn)H,作BD⊥AC,垂足為點(diǎn)D,根據(jù)垂徑定理得出MN=2MH,PM=PN,再利用勾股定理求出PH、AH、MH、MN的長(zhǎng),從而求出AM、NC的長(zhǎng),然后求出![]() 、
、![]() 的值,得出
的值,得出![]() =
=![]() ,利用兩邊對(duì)應(yīng)成比例且?jiàn)A角相等的兩三角形相似即可證明.
,利用兩邊對(duì)應(yīng)成比例且?jiàn)A角相等的兩三角形相似即可證明.
(1)如圖,作BD⊥AC,垂足為點(diǎn)D,
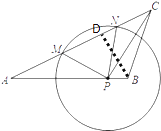
∵⊙P與邊AC相切,
∴BD就是⊙P的半徑,
在Rt△ABD中,tanA= ![]() ,
,
設(shè)BD=x,則AD=2x,
∴x2+(2x)2=152,
解得:x=3![]() ,
,
∴半徑為3![]() ;
;
(2)相似,理由見(jiàn)解析,
如圖,過(guò)點(diǎn)P作PH⊥AC于點(diǎn)H,作BD⊥AC,垂足為點(diǎn)D,
∴PH垂直平分MN,
∴PM=PN,
在Rt△AHP中,tanA=![]() ,
,
設(shè)PH=y,AH=2y,
y2+(2y)2=(6![]() )2
)2
解得:y=6(取正數(shù)),
∴PH=6,AH=12,
在Rt△MPH中,
MH=![]() =3,
=3,
∴MN=2MH=6,
∴AM=AH-MH=12-3=9,
NC=AC-MN-AM=20-6-9=5,
∴![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
又∵PM=PN,
∴∠PMN=∠PNM,
∴∠AMP=∠PNC,
∴△AMP∽△PNC.




| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】李莉在五張完全相同并且沒(méi)有任何標(biāo)記的卡片的一面分別寫(xiě)下數(shù)據(jù)﹣4,﹣1,0,3,5,將寫(xiě)有數(shù)據(jù)的一面朝下放置,并混合均勻.
(1)隨機(jī)摸起一張,求上面的數(shù)據(jù)為負(fù)數(shù)的概率;
(2)隨機(jī)摸起兩張,其中一張表示x,另一張表示y,求點(diǎn)(x,y)在直線(xiàn)y=﹣x﹣1上的概率;
(3)隨機(jī)摸起一張,記為x,然后放回,混合均勻后再隨機(jī)摸起一張,記為y,求點(diǎn)(x,y)是第四象限內(nèi)的點(diǎn)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:對(duì)角線(xiàn)互相垂直且相等的四邊形叫做垂等四邊形.
(1)下面四邊形是垂等四邊形的是____________(填序號(hào))
①平行四邊形;②矩形;③菱形;④正方形
(2)圖形判定:如圖1,在四邊形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,過(guò)點(diǎn)D作BD垂線(xiàn)交BC的延長(zhǎng)線(xiàn)于點(diǎn)E,且
,過(guò)點(diǎn)D作BD垂線(xiàn)交BC的延長(zhǎng)線(xiàn)于點(diǎn)E,且![]() ,證明:四邊形
,證明:四邊形![]() 是垂等四邊形.
是垂等四邊形.
(3)由菱形面積公式易知性質(zhì):垂等四邊形的面積等于兩條對(duì)角線(xiàn)乘積的一半.應(yīng)用:在圖2中,面積為24的垂等四邊形![]() 內(nèi)接于⊙O中,
內(nèi)接于⊙O中,![]() .求⊙O的半徑.
.求⊙O的半徑.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
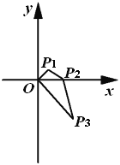
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() 的坐標(biāo)
的坐標(biāo) ,將線(xiàn)段
,將線(xiàn)段![]() 繞點(diǎn)
繞點(diǎn)![]() 按順時(shí)針?lè)较蛐D(zhuǎn)45°,再將其長(zhǎng)度伸長(zhǎng)為
按順時(shí)針?lè)较蛐D(zhuǎn)45°,再將其長(zhǎng)度伸長(zhǎng)為![]() 的2倍,得到線(xiàn)段
的2倍,得到線(xiàn)段![]() ;又將線(xiàn)段
;又將線(xiàn)段![]() 繞點(diǎn)
繞點(diǎn)![]() 按順時(shí)針?lè)较蛐D(zhuǎn)45°,長(zhǎng)度伸長(zhǎng)為
按順時(shí)針?lè)较蛐D(zhuǎn)45°,長(zhǎng)度伸長(zhǎng)為![]() 的2倍,得到線(xiàn)段
的2倍,得到線(xiàn)段![]() ;如此下去,得到線(xiàn)段
;如此下去,得到線(xiàn)段![]() 、
、![]() ,……,
,……,![]() (
(![]() 為正整數(shù)),則點(diǎn)
為正整數(shù)),則點(diǎn)![]() 的坐標(biāo)是_________.
的坐標(biāo)是_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】圖1是一個(gè)地鐵站入口的雙翼閘機(jī).如圖2,它的雙翼展開(kāi)時(shí),雙翼邊緣的端點(diǎn)A與B之間的距離為10cm,雙翼的邊緣AC=BD=54cm,且與閘機(jī)側(cè)立面夾角∠PCA=∠BDQ=30°.當(dāng)雙翼收起時(shí),可以通過(guò)閘機(jī)的物體的最大寬度為( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
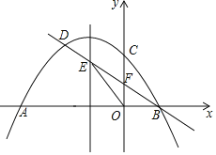
【題目】如圖,拋物線(xiàn)![]() 與x軸交于A、B兩點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C,過(guò)點(diǎn)B的直線(xiàn)與拋物線(xiàn)的另一個(gè)交點(diǎn)為D,與拋物線(xiàn)的對(duì)稱(chēng)軸交于點(diǎn)E,與y軸交于點(diǎn)F,且
與x軸交于A、B兩點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C,過(guò)點(diǎn)B的直線(xiàn)與拋物線(xiàn)的另一個(gè)交點(diǎn)為D,與拋物線(xiàn)的對(duì)稱(chēng)軸交于點(diǎn)E,與y軸交于點(diǎn)F,且![]() ,△OBE的面積為
,△OBE的面積為![]() .
.
(1)求拋物線(xiàn)的解析式;
(2)設(shè)P為已知拋物線(xiàn)上的任意一點(diǎn),當(dāng)△ACP的面積等于△ACB的面積時(shí),求點(diǎn)P的坐標(biāo);
(3)點(diǎn)Q(0,m)是y軸上的動(dòng)點(diǎn),連接AQ、BQ,當(dāng)∠AQB為鈍角時(shí),則m的取值范圍是 .(直接寫(xiě)出答案)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直角坐標(biāo)系xOy中,一次函數(shù)y=﹣![]() x+5的圖象l1分別與x,y軸交于A,B兩點(diǎn),正比例函數(shù)的圖象l2與l1交于點(diǎn)C(m,4).
x+5的圖象l1分別與x,y軸交于A,B兩點(diǎn),正比例函數(shù)的圖象l2與l1交于點(diǎn)C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函數(shù)y=kx+1的圖象為l3,且11,l2,l3不能?chē)扇切危苯訉?xiě)出k的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,是根據(jù)某市2010年至2014年工業(yè)生產(chǎn)總值繪制的折線(xiàn)統(tǒng)計(jì)圖,觀(guān)察統(tǒng)計(jì)圖獲得以下信息,其中信息判斷錯(cuò)誤的是( )

A.2010年至2014年間工業(yè)生產(chǎn)總值逐年增加
B.2014年的工業(yè)生產(chǎn)總值比前一年增加了40億元
C.2012年與2013年每一年與前一年比,其增長(zhǎng)額相同
D.從2011年至2014年,每一年與前一年比,2014年的增長(zhǎng)率最大
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com