
【題目】某校為響應(yīng)我市全民閱讀活動,利用節(jié)假日面向社會開放學(xué)校圖書館.據(jù)統(tǒng)計,第一個月進(jìn)館128人次,進(jìn)館人次逐月增加,到第三個月末累計進(jìn)館608人次,若進(jìn)館人次的月平均增長率相同.
(1)求進(jìn)館人次的月平均增長率;
(2)因條件限制,學(xué)校圖書館每月接納能力不超過500人次,在進(jìn)館人次的月平均增長率不變的條件下,校圖書館能否接納第四個月的進(jìn)館人次,并說明理由.
【答案】(1)進(jìn)館人次的月平均增長率為50%;(2)校圖書館能接納第四個月的進(jìn)館人次,見解析
【解析】
(1)先分別表示出第二個月和第三個月的進(jìn)館人次,再根據(jù)第一個月的進(jìn)館人次加第二和第三個月的進(jìn)館人次等于608,列方程求解;
(2)根據(jù)(1)所計算出的月平均增長率,計算出第四個月的進(jìn)館人次,再與500比較大小即可.
(1)設(shè)進(jìn)館人次的月平均增長率為x,則由題意得:128+128(1+x)+128(1+x)2=608,化簡得:4x2+12x-7=0,
∴(2x-1)(2x+7)=0,
∴x1=0.5=50%,x2=-3.5(舍去).
答:進(jìn)館人次的月平均增長率為50%.
(2)∵進(jìn)館人次的月平均增長率為50%,
∴第四個月的進(jìn)館人次為:128×(1+50%)3=128×![]() =432<500,
=432<500,
答:校圖書館能接納第四個月的進(jìn)館人次.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點P是菱形ABCD的對角線BD上一點,連接CP并延長,交AD于E,交BA的延長線于點F.
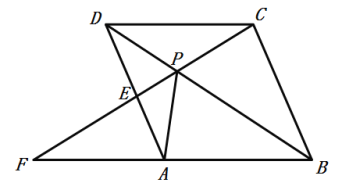
(1)求證:![]() .
.
(2)如果![]() ,求線段PC的長.
,求線段PC的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
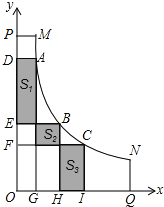
【題目】六一兒童節(jié),小文到公園游玩.看到公園的一段人行彎道MN(不計寬度),如圖,它與兩面互相垂直的圍墻OP、OQ之間有一塊空地MPOQN(MP⊥OP,NQ⊥OQ),他發(fā)現(xiàn)彎道MN上任一點到兩邊圍墻的垂線段與圍墻所圍成的矩形的面積都相等,比如:A、B、C是彎道MN上的三點,矩形ADOG、矩形BEOH、矩形CFOI的面積相等.愛好數(shù)學(xué)的他建立了平面直角坐標(biāo)系(如圖),圖中三塊陰影部分的面積分別記為S1、S2、S3,并測得S2=6(單位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)設(shè)T(x,y)是彎道MN上的任一點,寫出y關(guān)于x的函數(shù)關(guān)系式;
(3)公園準(zhǔn)備對區(qū)域MPOQN內(nèi)部進(jìn)行綠化改造,在橫坐標(biāo)、縱坐標(biāo)都是偶數(shù)的點處種植花木(區(qū)域邊界上的點除外),已知MP=2米,NQ=3米.問一共能種植多少棵花木?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD中,AB=4,BC=2,O為對角線AC的中點,點P、Q分別從A和B兩點同時出發(fā),在邊AB和BC上勻速運動,并且同時到達(dá)終點B、C,連接PO、QO并延長分別與CD、DA交于點M、N.在整個運動過程中,圖中陰影部分面積的大小變化情況是( )

A. 一直增大 B. 一直減小 C. 先減小后增大 D. 先增大后減小
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將一個直角三角形紙片![]() 放置在平面直角坐標(biāo)系中,已知點
放置在平面直角坐標(biāo)系中,已知點![]() ,點
,點![]() ,點
,點![]() .
.![]() 是邊
是邊![]() 上的一動點(點
上的一動點(點![]() 不與點
不與點![]() 、
、![]() 重合),沿著
重合),沿著![]() 折疊該紙片,得點
折疊該紙片,得點![]() 的對應(yīng)點
的對應(yīng)點![]() .
.
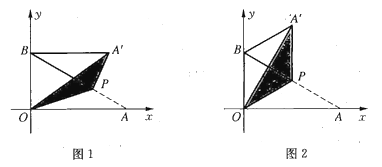
(1)如圖1,當(dāng)點![]() 在第一象限,且滿足
在第一象限,且滿足![]() 時,求點
時,求點![]() 的坐標(biāo);
的坐標(biāo);
(2)如圖2,當(dāng)![]() 為
為![]() 中點時,求
中點時,求![]() 的長;
的長;
(3)當(dāng)![]() 時,直接寫出點
時,直接寫出點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
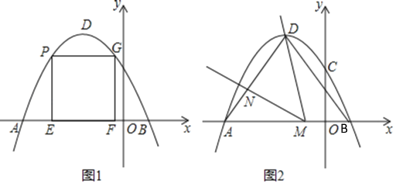
【題目】如圖1,在平面直角坐標(biāo)系中,拋物線y=﹣![]() x2+bx+c經(jīng)過點A(﹣5,0)和點B(1,0).
x2+bx+c經(jīng)過點A(﹣5,0)和點B(1,0).
(1)求拋物線的解析式及頂點D的坐標(biāo);
(2)點P是拋物線上A、D之間的一點,過點P作PE⊥x軸于點E,PG⊥y軸,交拋物線于點G,過點G作GF⊥x軸于點F,當(dāng)矩形PEFG的周長最大時,求點P的橫坐標(biāo);
(3)如圖2,連接AD、BD,點M在線段AB上(不與A、B重合),作∠DMN=∠DBA,MN交線段AD于點N,是否存在這樣點M,使得△DMN為等腰三角形?若存在,求出AN的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點![]() 是反比例函數(shù)
是反比例函數(shù)![]() 圖象上的一點,過點
圖象上的一點,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() ,
,![]() 的面積為2.點
的面積為2.點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .若一次函數(shù)
.若一次函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() ,交雙曲線的另一支于點
,交雙曲線的另一支于點![]() ,交
,交![]() 軸點
軸點![]() .
.
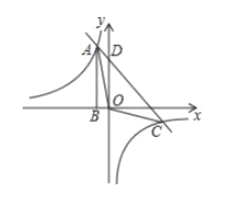
(1)求反比例函數(shù)和一次函數(shù)的解析式;
(2)若![]() 為
為![]() 軸上的一個動點,且
軸上的一個動點,且![]() 的面積為5,請求出點
的面積為5,請求出點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了預(yù)防“甲型H1N1”,某校對教室采用藥薰消毒法進(jìn)行消毒,已知藥物燃燒時,室內(nèi)每立方米空氣中的含藥量y(mg)與時間x(min)成正比例,藥物燃燒后,y與x成反比例,如圖所示,現(xiàn)測得藥物8min燃畢,此時室內(nèi)空氣每立方米的含藥量為6mg,請你根據(jù)題中提供的信息,解答下列問題:
(1)藥物燃燒時,求y關(guān)于x的函數(shù)關(guān)系式?自變量x的取值范圍是什么?藥物燃燒后y與x的函數(shù)關(guān)系式呢?
(2)研究表明,當(dāng)空氣中每立方米的含藥量低于1.6mg時,生方可進(jìn)教室,那么從消毒開始,至少需要幾分鐘后,生才能進(jìn)入教室?
(3)研究表明,當(dāng)空氣中每立方米的含藥量不低于3mg且持續(xù)時間不低于10min時,才能殺滅空氣中的毒,那么這次消毒是否有效?為什么?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標(biāo)分別為A(1,1),B(4,2),C(3,4)
(1)請畫出將△ABC向左平移4個單位長度后得到的圖形△A1B1C1;
(2)請畫出△ABC關(guān)于原點O成中心對稱的圖形△A2B2C2;
(3)在x軸上找一點P,使PA+PB的值最小,請直接寫出點P的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com