
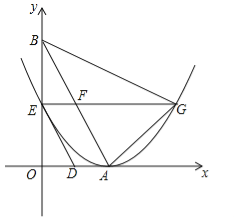
【題目】如圖,直線![]() 與x軸,y軸分別交于點A,點B,兩動點D,E分別從點A,點B同時出發(fā)向點O運動(運動到點O停止),運動速度分別是1個單位長度/秒和
與x軸,y軸分別交于點A,點B,兩動點D,E分別從點A,點B同時出發(fā)向點O運動(運動到點O停止),運動速度分別是1個單位長度/秒和![]() 個單位長度/秒,設(shè)運動時間為t秒,以點A為頂點的拋物線經(jīng)過點E,過點E作x軸的平行線,與拋物線的另一個交點為點G,與AB相交于點F.
個單位長度/秒,設(shè)運動時間為t秒,以點A為頂點的拋物線經(jīng)過點E,過點E作x軸的平行線,與拋物線的另一個交點為點G,與AB相交于點F.
(1)求點A,點B的坐標;
(2)用含t的代數(shù)式分別表示EF和AF的長;
(3)當四邊形ADEF為菱形時,試判斷△AFG與△AGB是否相似,并說明理由.
(4)是否存在t的值,使△AGF為直角三角形?若存在,求出這時拋物線的解析式;若不存在,請說明理由.
【答案】(1)A(2,0),B(0,![]() );(2)EF=t,AF=4﹣2t;(3)相似;(4)
);(2)EF=t,AF=4﹣2t;(3)相似;(4)![]() .
.
【解析】(1)在直線![]() 中,令y=0可得
中,令y=0可得![]() ,解得x=2,令x=0可得y=
,解得x=2,令x=0可得y=![]() ,∴A為(2,0),B為(0,
,∴A為(2,0),B為(0,![]() );
);
(2)由(1)可知OA=2,OB=![]() ,∴tan∠ABO=
,∴tan∠ABO=![]() =
=![]() ,∴∠ABO=30°,∵運動時間為t秒,∴BE=
,∴∠ABO=30°,∵運動時間為t秒,∴BE=![]() t,∵EF∥x軸,∴在Rt△BEF中,EF=BEtan∠ABO=
t,∵EF∥x軸,∴在Rt△BEF中,EF=BEtan∠ABO=![]() BE=t,BF=2EF=2t,在Rt△ABO中,OA=2,OB=
BE=t,BF=2EF=2t,在Rt△ABO中,OA=2,OB=![]() ,∴AB=4,∴AF=4﹣2t;
,∴AB=4,∴AF=4﹣2t;
(3)相似.理由如下:
當四邊形ADEF為菱形時,則有EF=AF,即t=4﹣2t,解得t=![]() ,∴AF=4﹣2t=4﹣
,∴AF=4﹣2t=4﹣![]() =
=![]() ,OE=OB﹣BE=
,OE=OB﹣BE=![]() =
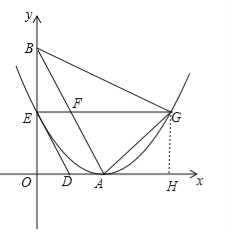
=![]() ,如圖,過G作GH⊥x軸,交x軸于點H,則四邊形OEGH為矩形,∴GH=OE=
,如圖,過G作GH⊥x軸,交x軸于點H,則四邊形OEGH為矩形,∴GH=OE=![]() ,又EG∥x軸,拋物線的頂點為A,∴OA=AH=2,在Rt△AGH中,由勾股定理可得
,又EG∥x軸,拋物線的頂點為A,∴OA=AH=2,在Rt△AGH中,由勾股定理可得![]() =
=![]() =
=![]() ,又AFAB=
,又AFAB=![]() ×4=
×4=![]() ,∴AFAB=AG2,即
,∴AFAB=AG2,即![]() ,且∠FAG=∠GAB,∴△AFG∽△AGB;
,且∠FAG=∠GAB,∴△AFG∽△AGB;
(4)存在,∵EG∥x軸,∴∠GFA=∠BAO=60°,又G點不能在拋物線的對稱軸上,∴∠FGA≠90°,∴當△AGF為直角三角形時,則有∠FAG=90°,又∠FGA=30°,∴FG=2AF,∵EF=t,EG=4,∴FG=4﹣t,且AF=4﹣2t,∴4﹣t=2(4﹣2t),解得t=![]() ,即當t的值為
,即當t的值為![]() 秒時,△AGF為直角三角形,此時OE=OB﹣BE=
秒時,△AGF為直角三角形,此時OE=OB﹣BE=![]() =
=![]() =
=![]() ,∴E點坐標為(0,
,∴E點坐標為(0,![]() ),∵拋物線的頂點為A,∴可設(shè)拋物線解析式為
),∵拋物線的頂點為A,∴可設(shè)拋物線解析式為![]() ,把E點坐標代入可得
,把E點坐標代入可得![]() =4a,解得a=
=4a,解得a=![]() ,∴拋物線解析式為
,∴拋物線解析式為![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知ABCD,AB>AD,分別以點A,C為圓心,以AD,CB長為半徑作弧,交AB,CD于點E,F(xiàn),連接AF,CE.求證:AF=CE.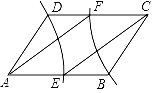
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)據(jù)9.30,9.05,9.10,9.40,9.20,9.10的眾數(shù)是;中位數(shù)是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 經(jīng)過點A(﹣3,0),點C(0,4),作CD∥x軸交拋物線于點D,作DE⊥x軸,垂足為E,動點M從點E出發(fā)在線段EA上以每秒2個單位長度的速度向點A運動,同時動點N從點A出發(fā)在線段AC上以每秒1個單位長度的速度向點C運動,當一個點到達終點時,另一個點也隨之停止運動,設(shè)運動時間為t秒.
經(jīng)過點A(﹣3,0),點C(0,4),作CD∥x軸交拋物線于點D,作DE⊥x軸,垂足為E,動點M從點E出發(fā)在線段EA上以每秒2個單位長度的速度向點A運動,同時動點N從點A出發(fā)在線段AC上以每秒1個單位長度的速度向點C運動,當一個點到達終點時,另一個點也隨之停止運動,設(shè)運動時間為t秒.
(1)求拋物線的解析式;
(2)設(shè)△DMN的面積為S,求S與t的函數(shù)關(guān)系式;
(3)①當MN∥DE時,直接寫出t的值;
②在點M和點N運動過程中,是否存在某一時刻,使MN⊥AD?若存在,直接寫出此時t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】點P為直線 ![]() 外一點,點A、B、C為直線
外一點,點A、B、C為直線 ![]() 上三點,PA=4cm,PB=5cm,PC=2cm,則點P到直線
上三點,PA=4cm,PB=5cm,PC=2cm,則點P到直線 ![]() 的距離為( )
的距離為( )
A.4cm
B.5cm
C.小于2cm
D.不大于2cm
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線經(jīng)過原點O,頂點為A(1,1),且與直線y=x﹣2交于B,C兩點.
(1)求拋物線的解析式及點C的坐標;
(2)求證:△ABC是直角三角形;
(3)若點N為x軸上的一個動點,過點N作MN⊥x軸與拋物線交于點M,則是否存在以O(shè),M,N為頂點的三角形與△ABC相似?若存在,請求出點N的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A、B的坐標分別為(8,0)、(0,![]() ),C是AB的中點,過點C作y軸的垂線,垂足為D,動點P從點D出發(fā),沿DC向點C勻速運動,過點P作x軸的垂線,垂足為E,連接BP、EC.當BP所在直線與EC所在直線第一次垂直時,點P的坐標為 .
),C是AB的中點,過點C作y軸的垂線,垂足為D,動點P從點D出發(fā),沿DC向點C勻速運動,過點P作x軸的垂線,垂足為E,連接BP、EC.當BP所在直線與EC所在直線第一次垂直時,點P的坐標為 .

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AC和BD相交于O點,若OA=OD,用“SAS”證明△AOB≌△DOC還需( ) 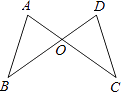
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com