
���}Ŀ����D��ʾ����ƽ��ֱ������ϵ�У���֪�cA(��1��0)�� B(0��![]() )������OAB�B�m(x��)�����D(zhu��n)׃�Q�����εõ���1����2����3����4�������t��2019��ֱ����c�����˞�______________��
)������OAB�B�m(x��)�����D(zhu��n)׃�Q�����εõ���1����2����3����4�������t��2019��ֱ����c�����˞�______________��

���𰸡�(2019+673![]() ��0)
��0)
��������
����(j��)���ɶ�����ʽ���AB���L���ٸ���(j��)���Ă��������c��һ�������ε�λ����ͬ��֪ÿ���������Ξ�һ��ѭ�h(hu��n)�M����ѭ�h(hu��n)��Ȼ�����һ��ѭ�h(hu��n)�M���D(zhu��n)ǰ�M���L�ȣ�����2019����3������(j��)�̞�673��֪��2019�������ε�ֱ����c��ѭ�h(hu��n)�M�����һ�������ε���c��������ɣ�
���cA(��1��0)�� B(0��![]() )��
)��
��AB��![]() ��
��
�ɈD��֪��ÿ���������Ξ�һ��ѭ�h(hu��n)�M����ѭ�h(hu��n)��һ��ѭ�h(hu��n)�Mǰ�M���L�Ȟ飺![]() ��2��1��3+
��2��1��3+![]() ��
��
��2019��3��673��
���2019��ֱ����c�ǵ�673��ѭ�h(hu��n)�M�����һ�������ε�ֱ����c��
��673����3+![]() ����2019+673
����2019+673![]() ��
��
���2019��ֱ����c�����˞飨2019+673![]() ��0����
��0����
�ʴ𰸞飺��2019+673![]() ��0����
��0����


 ��ĩ���Y(ji��)̖ϵ�д�
��ĩ���Y(ji��)̖ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D��Rt��ABC�У���ACB��90�㣬AC��BC������AB�����cO������ԭ�c��AB����ֱ����x�S������ƽ��ֱ������ϵ�У�����ABC�@�cB형r����D(zhu��n)��ʹ�cA���D(zhu��n)��y�S�������S�ϵ��cA'̎����AO��OB��2���t�D���Ӱ������e��_____��
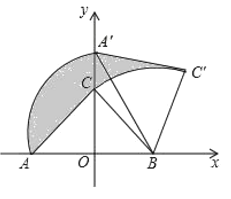
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ���ڌWУ�M����������������֪�R��ِ�У�8��1����8��2������ِ�˔�(sh��)��ͬ���ɿ��֞�A��B��C�����ȼ������������ȼ��ĵ÷�����ӛ��A��100�֡�B��90�֡�C��80�֣��_��B�����ϣ���B�����郞(y��u)�㣬����8��2������2���_��A�������ɂ���ijɿ��������L�Ƴ����µĽy(t��ng)Ӌ�D��Ո������І��}��

��1���������ِ�˔�(sh��)�����aȫ�l�νy(t��ng)Ӌ�D��
��2���˴θ�ِ��8��2����ɿ�?y��u)?/span>C�����˔�(sh��)��_______�ˣ�
��3��С��ͬ�W����(j��)������Ϣ���������½y(t��ng)Ӌ����
ƽ����(sh��)���֣� | ��λ��(sh��)���֣� | ���� | |
8��1���� | m | 90 | n |
8��2���� | 91 | 90 | 29 |
Ո�քe���m��n��ֵ�����ă�(y��u)���ʺͷ�(w��n)���Է�����^�ɂ���ijɿ���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ������AOBC�У�OB��4��OA��3���քe��OB��OA����ֱ����x�S��y�S��������D1��ʾ��ƽ��ֱ������ϵ��F��BC߅��һ�����c�����cB��C�غϣ����^�cF�ķ���������(sh��)y��![]() ��k��0���ĈD���c߅AC�����cE��
��k��0���ĈD���c߅AC�����cE��
��1�����cF�\�ӵ�߅BC�����c�r���cE�����˞�__________��
��2���B��EF�����EFC������ֵ��
��3����D2������CEF��EF�ۯB���cCǡ������߅OB�ϵ��cG̎����BG���L�ȣ�
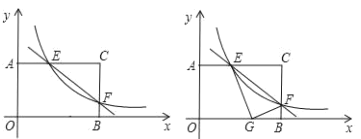
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D�������o�ķ����У�ÿ��С�����ε�߅�L����1����߅��![]() ��ƽ����߅�Σ��B�Y(ji��)
��ƽ����߅�Σ��B�Y(ji��)![]() ���c
���c![]() ��
��![]() ��
��![]() ��
��![]() ���ڸ��c�ϣ���Ո��Ҫ������������D�΄գ�Ҫ�كH�ßo�̶�ֱ�ߣ��Ҳ�����ֱ���е�ֱ�ǣ��ڱ������D���E��
���ڸ��c�ϣ���Ո��Ҫ������������D�΄գ�Ҫ�كH�ßo�̶�ֱ�ߣ��Ҳ�����ֱ���е�ֱ�ǣ��ڱ������D���E��
��1���ڈD1����![]() ����λ��
�����![]() ����
����![]() ��
��
��2���ڈD2��ȡ߅![]() ���c
���c![]() ����
����![]() ��
��![]() ����߅��
����߅��![]() ����
����![]() ����e����
����e����![]() ����e��
����e��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D���cC����AB��ֱ������O��һ�c��CD����O�о���D��AB�����L���ϣ���AE��CD��E��
��1�����C��ACƽ����BAE��
��2����AC=2CE=6������O�İ돽��
��3��Ո?zh��)���������AD��BD��CD֮�g�кΔ�(sh��)���Pϵ��Ո�C����ĽY(ji��)Փ��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ��(1)��D1����ABC����CDE�����߅�����Σ�ֱ��AD��ֱ��BE�����cF��
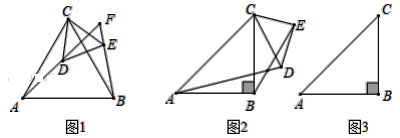
�����C��AD��BE��
�����AFB�ĶȔ�(sh��)��
(2)��D2����ABC����CDE�������ֱ�������Σ���ABC����DEC��90����ֱ��AD��ֱ��BE�����cF��
�����C��AD��![]() BE��
BE��
����AB��BC��3��DE��EC��![]() ������CDE�@���cC��ƽ���(n��i)���D(zhu��n)�����cD���ھ���BC�ϕr���ڈD3�Ю����D�Σ�����BF���L�ȣ�
������CDE�@���cC��ƽ���(n��i)���D(zhu��n)�����cD���ھ���BC�ϕr���ڈD3�Ю����D�Σ�����BF���L�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
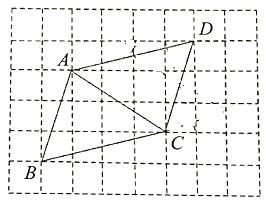
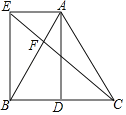
���}Ŀ����D������ABC�У�AB��AC��D��BC���c��AE��BD����AE��BD��
��1�����C����߅��AEBD�Ǿ��Σ�
��2���B��CE��AB���cF������ABE��30����AE��2����EF���L��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
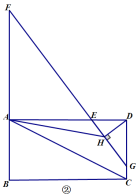
���}Ŀ����߅��![]() ����Σ��B��
������B��![]() ��
��![]() ���c
���c![]() ��
��![]() ߅�ϣ�
߅�ϣ�
��1����D�٣���![]() ��
��![]() ����
����![]() ����e��
����e��
��2����D�ڣ����L![]() ���c
���c![]() ��ʹ��
��ʹ��![]() ���B��
���B��![]() �����L��
�����L��![]() ���c
���c![]() ���^�c
���^�c![]() ��
��![]() ���c
���c![]() ���B��
���B��![]() �����C��
�����C��![]() ��
��
��3����D�ۣ�������![]() �@�c
�@�c![]() ���D(zhu��n)һ���ĽǶ�
���D(zhu��n)һ���ĽǶ�![]() ��
��![]() ���õ�����
���õ�����![]() ���B��
���B��![]() ���c
���c![]() ʼ�K��
ʼ�K��![]() �����c���B��
�����c���B��![]() ����֪
����֪![]() ��ֱ�ӌ���
��ֱ�ӌ���![]() ��ȡֵ������
��ȡֵ������


�鿴�𰸺ͽ���>>
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙��e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com