【題目】關于一次函數
，下列說法正確的是（ ）
A.它的圖象過點
B.它的圖象經過第一、二、三象限
C.
隨
的增大而增大D.當
時，總有
【答案】D
【解析】
A、利用一次函數圖象上點的坐標特征可得出點（1，-2）不在一次函數y=1-2x的圖象上，A不符合題意；
B、由k，b的值，利用一次函數圖象與系數的關系可得出一次函數y=1-2x的圖象經過第一、二、四象限，B不符合題意；
C、由k=-2＜0，利用一次函數的性質可得出y隨x的增大而減小，C不符合題意；
D、利用一次函數圖象上點的坐標特征以及一次函數的性質，可得出當x＞0時，總有y＜1，D符合題意．
此題得解．
解：
、當
時，
，
點
不在一次函數
的圖象上，不符合題意；
、
，
，
一次函數的圖象經過第一、二、四象限，不符合題意；
、，
隨
的增大而減小，不符合題意；
、
當
時，
，
當
時，總有
，符合題意．
故選：．
百年學典課時學練測系列答案科目：初中數學 來源： 題型：
【題目】下列說法：
“明天降雨的概率是
”表示明天有半天都在降雨；
無理數是開方開不盡的數；
若
為實數，則
是不可能事件；
的平方根是
，用式子表示是
；
某班的5位同學在向“創建圖書角”捐款活動中，捐款數如下（單位：元）：8，3，8，2，4，那么這組數據的眾數是8，中位數是4，平均數是5．其中正確的個數有（ ）
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】王老師為學校新年聯歡會購買獎品，在某文具用品店購買明信片，每一張明信片的價格是8元，在結算時發現，如果再多買5張，就可以享受到打九折的優惠，總價格反而減少8元，為了能享受優惠，王老師比原計劃多購買了5張明信片；
（1）王老師實際購買多少張明信片？一共花了多少錢？
（2）文具店開展元旦優惠活動：從即日起，在一周內，憑購物小票，累計購物超過500元，超過部分可以享受八折的優惠．王老師想了一想，又為學校購買了一定數量的筆記本，享受了八折優惠，這樣，兩次一共節省了36元，王老師購買筆記本實際花了多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線 y1 與 y2 相交于點C ， y1 與 x 軸交于點 D ，與 y 軸交于點0,1， y2 與 x 軸 交于點 B3,0，與 y 軸交于點 A ，下列說法正確的個數有（ ）
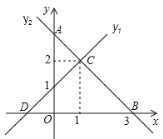
①y1的 解 析 式 為
；② OA OB ；③
；④
；⑤ AOB BCD .
A.2 個B.3個C.4 個D.5 個
查看答案和解析>>
科目：初中數學 來源： 題型：
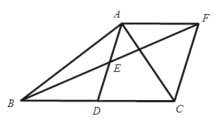
【題目】如圖，在ABC 中， AD 是 BC 邊上的中線，點 E 是 AD 的中點，過點 A 作AF // BC 交 BE 的延長線于 F ，連接CF .
（1）求證： AEF DEB ；
（2）若BAC 90，試判斷四邊形 ADCF 的形狀，并證明你的結論；
（3）在（2）的情況下，如果 AC 2 ，點 M 在 AC 線段上移動，當 MB MD 有最小值時，求 AM 的長度（提示：以 D 點為原點， AD 為 y 正半軸， DC 為 x 正軸建立平面直角坐標系）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一個梯子AB長2.5米，頂端A靠在墻AC上，這時梯子下端B與墻角C距離為1.5米，梯子滑動后停在DE的位置上，測得BD長為0.5米，則梯子頂端A下落了（ ）米．
A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，用火柴棒擺出一列正方形圖案，第①個圖案用了 4 根，第②個圖案用了 12 根，第③個圖案用了 24 根，按照這種方式擺下去，擺出第⑥個圖案用火柴棒的根數是（ ）
A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目：初中數學 來源： 題型：
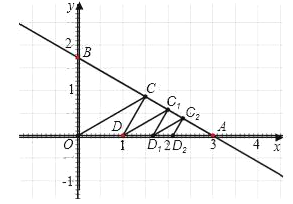
【題目】如圖，在平面直角坐標系中，直線
交x軸于A點，交y軸于B點，點C是線段AB的中點，連接OC，然后將直線OC繞點C逆時針旋轉30°交x軸于點D，再過D點作直線DC1∥OC，交AB與點C1，然后過C1點繼續作直線D1C1∥DC，交x軸于點D1，并不斷重復以上步驟，記△OCD的面積為S1，△DC1D1的面積為S2，依此類推，后面的三角形面積分別是S3，S4…，那么S1=_____，若S=S1+S2+S3+…+Sn，當n無限大時，S的值無限接近于_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①所示，在直角梯形ABCD中，∠BAD=90°，E是直線AB上一點，過E作直線l∥BC，交直線CD于點F．將直線l向右平移，設平移距離BE為t（t≥0），直角梯形ABCD被直線l掃過的面積（圖中陰影部分）為S，S關于t的函數圖象如圖②所示，OM為線段，MN為拋物線的一部分，NQ為射線，N點橫坐標為4．
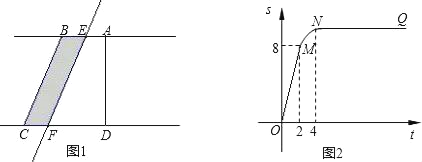
信息讀取
（1）梯形上底的長AB= ；
（2）直角梯形ABCD的面積= ；
圖象理解
（3）寫出圖②中射線NQ表示的實際意義；
（4）當2＜t＜4時，求S關于t的函數關系式；
問題解決
（5）當t為何值時，直線l將直角梯形ABCD分成的兩部分面積之比為1：3．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com