Question

【題目】已知是等邊三角形.

（1）將繞點逆時針旋轉角（）；得到，和所在直線相交于點.

①如圖，當時，與是否全等？ （填“是”或“否”）， 度；

②當旋轉到如圖所在位置時，求的度數；

（2）如圖，在和上分別截取點和，使，，連接，將繞點逆時針旋轉角（），得到，和所在直線相交于點，請利用圖探索的度數，直接寫出結果，不必說明理由.

Answer 1

【答案】（1）①是， 120；②120°；（2）當時，；當時，.

【解析】

（1）①根據旋轉變換的性質以及等邊三角形的性質可得AB=AD=AC=AE，∠BAD=∠CAE，然后利用“邊角邊”證明△ABD與△ACE全等；根據三角形的內角和等于180°求出∠ABD與∠AEC的度數，再根據旋轉角為20°求出∠BAE的度數，然后利用四邊形的內角和公式求解即可；

②先利用“邊角邊”證明△BAD和△CAE全等，根據全等三角形對應角相等可得∠ADB=∠AEC，再利用四邊形ABOE的內角和等于360°推出∠BOE+∠DAE=180°，再根據等邊三角形的每一個角都是60°得到∠DAE=60°，從而得解；

（2）先求出B′C′∥BC，證明△AB′C′是等邊三角形，再根據旋轉變換的性質可得AD=AE，∠BAD=∠CAE，然后利用“邊角邊”證明△ABD和△ACE全等，根據全等三角形對應角相等可得∠ABD=∠ACE，再利用三角形的內角和定理求出∠BOC的度數，然后分0°＜θ≤30°與30°＜θ＜180°兩種情況求解．

（1）①∵△ADE是由△ABC繞點A旋轉θ得到，△ABC是等邊三角形，

∴AB=AD=AC=AE，∠BAD=∠CAE=20°，

在△ABD與△ACE中，

，

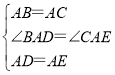∴△ABD≌△ACE（SAS）；

∵θ=20°，

∴∠ABD=∠AEC=（180°-20°）=80°，

又∵∠BAE=θ+∠BAC=20°+60°=80°，

∴在四邊形ABOE中，∠BOE=360°-80°-80°-80°=120°；

②由已知得：△ABC和△ADE是全等的等邊三角形，

∴AB=AD=AC=AE，

∵△ADE是由△ABC繞點A旋轉θ得到的，

∴∠BAD=∠CAE=θ，

∴△BAD≌△CAE，

∴∠ADB=∠AEC，

∵∠ADB+∠ABD+∠BAD=180°，

∴∠AEC+∠ABD+∠BAD=180°，

∵∠ABO+∠AEC+∠BAE+∠BOE=360°，

∵∠BAE=∠BAD+∠DAE，

∴∠DAE+∠BOE=180°，

又∵∠DAE=60°，

∴∠BOE=120°；

（2）如圖，∵AB=AB′，AC=AC′，

∴，

∴B′C′∥BC，

∵△ABC是等邊三角形，

∴△AB′C′是等邊三角形，

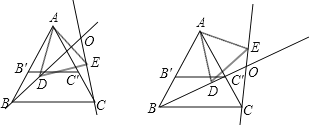
根據旋轉變換的性質可得AD=AE，∠BAD=∠CAE，

在△ABD和△ACE中，

，

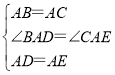∴△ABD≌△ACE（SAS），

∴∠ABD=∠ACE，

∴∠BOC=180°-（∠OBC+∠OCB），

=180°-（∠OBC+∠ACB+∠ACE），

=180°-（∠OBC+∠ACB+∠ABD），

=180°-（∠ACB+∠ABC），

=180°-（60°+60°），

=60°，

當時，∠BOE=∠BOC=60°，

當30°＜θ＜180°時，∠BOE=180°-∠BOC=180°-60°=120°．