
【題目】對于一次函數(shù)![]()
![]() ,我們稱函數(shù)
,我們稱函數(shù)![]()
![]()
為它的m分函數(shù)(其中m為常數(shù)).
例如,![]() 的4分函數(shù)為:當(dāng)
的4分函數(shù)為:當(dāng)![]() 時,
時,![]() ;當(dāng)
;當(dāng)![]() 時,
時,![]() .
.
(1)如果![]() 的2分函數(shù)為
的2分函數(shù)為![]() ,
,
① 當(dāng)![]() 時,
時,![]() ; ②當(dāng)
; ②當(dāng)![]() 時,
時,![]() .
.
(2)如果![]() 的-1分函數(shù)為
的-1分函數(shù)為![]() ,求雙曲線
,求雙曲線![]() 與
與![]() 的圖象的交點坐標(biāo);
的圖象的交點坐標(biāo);
(3)從下面兩問中任選一問作答:
①設(shè)y=x+2的m分函數(shù)為y![]() ,如果拋物線y=x
,如果拋物線y=x![]() 與y
與y![]() 的圖象有且只有一個公共點,直接寫出m的取值范圍。
的圖象有且只有一個公共點,直接寫出m的取值范圍。
②如果點A(0,t)到y=x+2的0分函數(shù)y[0]的圖象的距離小于1,直接寫出t的取值范圍。
【答案】(1)①3,②4或-2;(2)(-2,-1);(3)①無解;②2<t<2+![]() ,2
,2![]() <t<2.
<t<2.
【解析】
(1)先寫出函數(shù)的2分函數(shù),代入即可,注意,函數(shù)值是3時分兩種情況代入;
(2)先寫出函數(shù)的-1分函數(shù),分兩種情況和雙曲線解析式聯(lián)立求解即可;
(3)①先寫出函數(shù)m分函數(shù),聯(lián)立方程組,轉(zhuǎn)化成方程求解即可,
②先寫出函數(shù)0分函數(shù),根據(jù)點到直線的距離公式求出t的范圍.
(1)y=x+1的2分函數(shù)為:當(dāng)x2時,y![]() =x+1;當(dāng)x>2時,y
=x+1;當(dāng)x>2時,y![]() =x1.
=x1.
當(dāng)x=4時,y![]() =41=3,
=41=3,
當(dāng)y![]() =3時,
=3時,
如果x2,則有,x+1=3,
∴x=2,
如果x>2,則有,x1=3,
∴x=4,
故答案為3,4或2;
(2)當(dāng)y=x+1的1分函數(shù)為y![]() ,
,
∴當(dāng)x1時,y![]() =x+1①,
=x+1①,
當(dāng)x>1時,y![]() =x1②,
=x1②,
∵雙曲線y=![]() ③,
③,
聯(lián)立①③解得,![]() ,
,
∴它們的交點坐標(biāo)為(2,1),
聯(lián)立②③時,方程無解,
∴雙曲線y=![]() 與y[1]的圖象的交點坐標(biāo)(2,1);
與y[1]的圖象的交點坐標(biāo)(2,1);
(3)①∵y=x+2的m分函數(shù)為y![]() ,
,
∴xm時,y![]() =x+2①,
=x+2①,
當(dāng)x>m時,y![]() =x2②,
=x2②,
∵拋物線y=x![]() ③與y
③與y![]() 的圖象有且只有一個公共點,
的圖象有且只有一個公共點,
聯(lián)立①③,則有x![]() =x+2,
=x+2,
∴x=2,或x=1,
∵只有一個公共點,
∴2m<1
聯(lián)立②③,![]() =x2,
=x2,
∴此方程無解,
②∵y=x+2的0分函數(shù)y![]() ,
,
∴當(dāng)x0時,y![]() =x+2,
=x+2,
∴d=![]() <1,
<1,
∴2![]() <t<2+
<t<2+![]() ,
,
∵x0,
∴2<t<2+![]() ,
,
當(dāng)x>0時,y![]() =x2,
=x2,
∴d=|0t2|![]() <1,
<1,
∴2![]() <t<2+
<t<2+![]() ,
,
∵x>0,
∴2![]() <t<2,
<t<2,
∴點A(0,t)到y=x+2的0分函數(shù)y![]() 的圖象的距離小于1,t的取值范圍2<t<2+
的圖象的距離小于1,t的取值范圍2<t<2+![]() ,2
,2![]() <t<2.
<t<2.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AC為直徑作![]() 交BC于點D,過點D作FE⊥AB于點E,交AC的延長線于點F.
交BC于點D,過點D作FE⊥AB于點E,交AC的延長線于點F.
(1)求證: EF與![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的長.
,求EB的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】商店要出售一種商品,出售時要在進(jìn)價的基礎(chǔ)上加上一定的利潤,其銷售量![]() (千克)與售價
(千克)與售價![]() (元)之間的關(guān)系如下表.
(元)之間的關(guān)系如下表.
銷量 | 售價 |
1 | 1+0.3+0.05 |
2 | 2+0.6+0.05 |
3 | 3+0.9+0.05 |
4 | 4+1.2+0.05 |
... | ... |
(1)寫出用含![]() 的式子表示售價
的式子表示售價![]() 的計算公式。
的計算公式。
(2)此商品的銷售量為10千克時,售價為多少?
(3)當(dāng)售價為26.05元時,商品的銷售量為多少千克?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一個數(shù)表有7行7列,設(shè)aij表示第i行第j列上的數(shù)(其中i=1, 2, 3, ...7,j=1, 2, 3, …,7)

例如:第5行第3列上的數(shù)a53=7.
則: (1) (a23 -a22)+(a52 –a53)= _________.
(2)此數(shù)表中的四個數(shù)anp,ank, amp,amk.滿足(anp -ank)+(amk -amp)=_ _________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,Rt△ABC的三個頂點分別是A(-4,2)、B(0,4)、C(0,2),
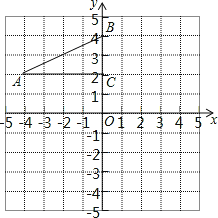
(1)畫出△ABC關(guān)于點C成中心對稱的△A1B1C;平移△ABC,若點A的對應(yīng)點A2的坐標(biāo)為(0,-4),畫出平移后對應(yīng)的△A2B2C2;
(2)△A1B1C和△A2B2C2關(guān)于某一點成中心對稱,則對稱中心的坐標(biāo)為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
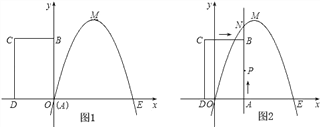
【題目】如圖,已知拋物線經(jīng)過坐標(biāo)原點O和x軸上另一點E,頂點M的坐標(biāo)為(2,4);矩形ABCD的頂點A與點O重合,AD、AB分別在x軸、y軸上,且AD=2,AB=3.
(1)求該拋物線所對應(yīng)的函數(shù)關(guān)系式;
(2)將矩形ABCD以每秒1個單位長度的速度從如圖所示的位置沿x軸的正方向勻速平行移動,同時一動點P也以相同的速度從點A出發(fā)向B勻速移動,設(shè)它們運動的時間為t秒(0≤t≤3),直線AB與該拋物線的交點為N(如圖2所示).
①當(dāng)t=![]() 時,判斷點P是否在直線ME上,并說明理由;
時,判斷點P是否在直線ME上,并說明理由;
②設(shè)以P、N、C、D為頂點的多邊形面積為S,試問S是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,點D,E分別是邊BC,AB上的中點,連接DE并延長至點F,使EF=2DF,連接CE、AF.
(1)證明:AF=CE;
(2)當(dāng)∠B=30°時,試判斷四邊形ACEF的形狀并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,矩形![]() 擺放在平面直角坐標(biāo)系中,點
擺放在平面直角坐標(biāo)系中,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上,
軸上,![]() ,
,![]() ,過點
,過點![]() 的直線交矩形
的直線交矩形![]() 的邊
的邊![]() 于點
于點![]() ,且點
,且點![]() 不與點
不與點![]() 、
、![]() 重合,過點
重合,過點![]() 作
作![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() .
.
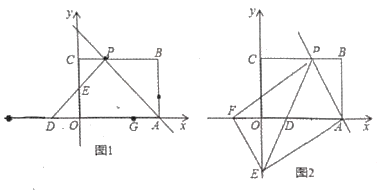
(Ⅰ)若![]() 為等腰直角三角形.
為等腰直角三角形.
①直接寫出此時![]() 點的坐標(biāo):______;直線
點的坐標(biāo):______;直線![]() 的解析式為______;
的解析式為______;
②在![]() 軸上另有一點
軸上另有一點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,請在直線
,請在直線![]() 和
和![]() 軸上分別找一點
軸上分別找一點![]() 、
、![]() ,使
,使![]() 的周長最小,并求出此時點
的周長最小,并求出此時點![]() 的坐標(biāo)和
的坐標(biāo)和![]() 周長的最小值.
周長的最小值.
(Ⅱ)如圖2,過點![]() 作
作![]() 交
交![]() 軸于點
軸于點![]() ,若以
,若以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形,求直線
為頂點的四邊形是平行四邊形,求直線![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】4月初某地豬肉價格大幅度下調(diào),下調(diào)后每千克豬肉的價格是原價格的![]() ,原來用120元買到的豬肉下調(diào)后可多買2kg.4月中旬豬肉價格開始回升,經(jīng)過兩個月后,豬肉價格上調(diào)為每千克28.8元.
,原來用120元買到的豬肉下調(diào)后可多買2kg.4月中旬豬肉價格開始回升,經(jīng)過兩個月后,豬肉價格上調(diào)為每千克28.8元.
(1)求4月初豬肉價格下調(diào)后變?yōu)槊壳Э硕嗌僭?/span>
(2)求5、6月份豬肉價格的月平均增長率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com