
【題目】如圖,直線y=﹣x+5與雙曲線![]() (x>0)相交于A,B兩點(diǎn),與x軸相交于C點(diǎn),△BOC的面積是
(x>0)相交于A,B兩點(diǎn),與x軸相交于C點(diǎn),△BOC的面積是![]() .若將直線y=﹣x+5向下平移1個單位,則所得直線與雙曲線
.若將直線y=﹣x+5向下平移1個單位,則所得直線與雙曲線![]() (x>0)的交點(diǎn)有( )
(x>0)的交點(diǎn)有( )

A. 0個B. 1個C. 2個D. 0個,或1個,或2個
【答案】B
【解析】
試題令直線y=﹣x+5與y軸的交點(diǎn)為點(diǎn)D,過點(diǎn)O作OE⊥直線AC于點(diǎn)E,過點(diǎn)B作BF⊥x軸于點(diǎn)F,如圖所示.
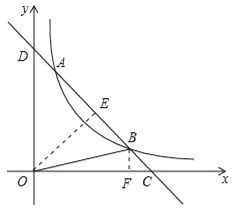
令直線y=﹣x+5中x=0,則y=5,即OD=5;
令直線y=﹣x+5中y=0,則0=﹣x+5,解得:x=5,即OC=5.
在Rt△COD中,∠COD=90°,OD=OC=5,∴tan∠DCO=![]() =1,∠DCO=45°.
=1,∠DCO=45°.
∵OE⊥AC,BF⊥x軸,∠DCO=45°,∴△OEC與△BFC都是等腰直角三角形,又∵OC=5,∴OE=![]() .∵S△BOC=
.∵S△BOC=![]() BCOE=
BCOE=![]() BC=
BC=![]() ,∴BC=
,∴BC=![]() ,∴BF=FC=
,∴BF=FC=![]() BC=1,∵OF=OC﹣FC=5﹣1=4,BF=1,∴點(diǎn)B的坐標(biāo)為(4,1),∴k=4×1=4,即雙曲線解析式為
BC=1,∵OF=OC﹣FC=5﹣1=4,BF=1,∴點(diǎn)B的坐標(biāo)為(4,1),∴k=4×1=4,即雙曲線解析式為![]() .
.
將直線y=﹣x+5向下平移1個單位得到的直線的解析式為y=﹣x+5﹣1=﹣x+4,將y=﹣x+4代入到![]() 中,得:
中,得:![]() ,整理得:
,整理得:![]() ,∵△=16﹣4×4=0,∴平移后的直線與雙曲線
,∵△=16﹣4×4=0,∴平移后的直線與雙曲線![]() 只有一個交點(diǎn).故選B.
只有一個交點(diǎn).故選B.


 開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
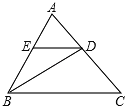
【題目】如圖,在△ABC中,BD是∠ABC的角平分線,DE∥BC,交AB于E,∠A=55°,∠BDC=95°,求△BDE各內(nèi)角的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上任意的點(diǎn)(不與端點(diǎn)重合),且
上任意的點(diǎn)(不與端點(diǎn)重合),且![]() ,連接
,連接![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,連接
,連接![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() .給出如下幾個結(jié)論:①
.給出如下幾個結(jié)論:①![]() ;②
;②![]() ;③
;③![]() 與
與![]() 一定不垂直;④
一定不垂直;④![]() 的大小為定值.其中正確的結(jié)論有________.
的大小為定值.其中正確的結(jié)論有________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某廣告公司設(shè)計(jì)一幅周長為16米的矩形廣告牌,廣告設(shè)計(jì)費(fèi)為每平方米2000元.設(shè)矩形一邊長為x,面積為S平方米.
(1)求S與x之間的函數(shù)關(guān)系式,并寫出自變量x的取值范圍;
(2)設(shè)計(jì)費(fèi)能達(dá)到24000元嗎?為什么?
(3)當(dāng)x是多少米時,設(shè)計(jì)費(fèi)最多?最多是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】設(shè)m是不小于﹣1的實(shí)數(shù),關(guān)于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有兩個不相等的實(shí)數(shù)根x1、x2,
(1)若x12+x22=6,求m值;
(2)令T=![]() ,求T的取值范圍.
,求T的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為4的等邊![]() 中,點(diǎn)D、E分別是邊AC和AB的一點(diǎn);
中,點(diǎn)D、E分別是邊AC和AB的一點(diǎn);
![]() 如圖1,當(dāng)
如圖1,當(dāng)![]() 時,連接BD、CE,設(shè)BD與CE交于點(diǎn)O,
時,連接BD、CE,設(shè)BD與CE交于點(diǎn)O,![]() 求證:
求證:![]() ;
;![]() 求
求![]() 的度數(shù);
的度數(shù);
![]() 如圖2,點(diǎn)F是邊BC的中點(diǎn),點(diǎn)D是邊AC的中點(diǎn),過F作
如圖2,點(diǎn)F是邊BC的中點(diǎn),點(diǎn)D是邊AC的中點(diǎn),過F作![]() 交邊AB于點(diǎn)E,連接DE,請你利用目前所學(xué)知識試說明:
交邊AB于點(diǎn)E,連接DE,請你利用目前所學(xué)知識試說明:![]() .
.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(操作發(fā)現(xiàn))
如圖①,在邊長為1個單位長度的小正方形組成的網(wǎng)格中,△ABC的三個頂點(diǎn)均在格點(diǎn)上.
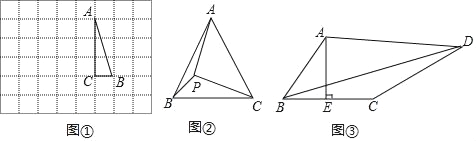
(1)請按要求畫圖:將△ABC繞點(diǎn)A按逆時針方向旋轉(zhuǎn)90°,點(diǎn)B的對應(yīng)點(diǎn)為B′,點(diǎn)C的對應(yīng)點(diǎn)為C′,連接BB′
(2)在(1)所畫圖形中,∠AB′B= .
(問題解決)
如圖②,在等邊三角形ABC中,AC=![]() ,點(diǎn)P在△ABC內(nèi),且∠APC=90°,∠BPC=120°,求△APC的面積.
,點(diǎn)P在△ABC內(nèi),且∠APC=90°,∠BPC=120°,求△APC的面積.
小明同學(xué)通過觀察、分析、思考,對上述問題形成了如下想法:
想法一:將△APC繞點(diǎn)A按順時針方向旋轉(zhuǎn)60°,得到△AP′B,連接PP′,尋找線段PA、PC之間的數(shù)量關(guān)系;
想法二:將△APB繞點(diǎn)A按逆時針方向旋轉(zhuǎn)60°,得到△AP′C′,連接PP′,尋找線段PA、PC之間的數(shù)量關(guān)系;
請參考小明同學(xué)的想法,完成該問題的解答過程.(求解一種方法即可)
(靈活運(yùn)用)
如圖③,在四邊形ABCD中,AE⊥BC,垂足為E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k為常數(shù)),直接寫出BD的長(用含k的式子表示).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 從
從![]() 開始沿折線
開始沿折線![]() 以
以![]() 的速度運(yùn)動,點(diǎn)
的速度運(yùn)動,點(diǎn)![]() 從
從![]() 開始沿
開始沿![]() 邊以
邊以![]() 的速度移動,如果點(diǎn)
的速度移動,如果點(diǎn)![]() 、
、![]() 分別從
分別從![]() 、
、![]() 同時出發(fā),當(dāng)其中一點(diǎn)到達(dá)
同時出發(fā),當(dāng)其中一點(diǎn)到達(dá)![]() 時,另一點(diǎn)也隨之停止運(yùn)動,設(shè)運(yùn)動時間為
時,另一點(diǎn)也隨之停止運(yùn)動,設(shè)運(yùn)動時間為![]() ,當(dāng)
,當(dāng)![]() ________時,四邊形
________時,四邊形![]() 也為矩形.
也為矩形.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,垂足為
,垂足為![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn).現(xiàn)有下列四個結(jié)論:①
的中點(diǎn).現(xiàn)有下列四個結(jié)論:①![]() ;②四邊形
;②四邊形![]() 的面積等于
的面積等于![]() ;③
;③![]() ;④
;④![]() .其中正確結(jié)論的個數(shù)為( )
.其中正確結(jié)論的個數(shù)為( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com