設2002x3＝2003y3＝2004z3，xyz＞0，且
，試求
的值．[方法提示：本題若直接去求x、y、z的值再代入求值是行不通的，只能由本題的特殊性，通過對已知條件的適當變換，求出的值，為此可設2002x3＝2002y3＝2002z3＝a(a≠0)，再通過適當的代數變形求出的值．]
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目：初中數學 來源： 題型：
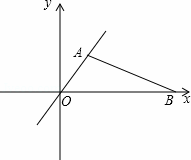
如圖，甲、乙兩人分別從A(1，
)、B(6，0)兩點同時出發，點O為坐標原點，甲沿AO方向、乙沿BO方向均以4km/h的速度行駛，th后，甲到達M點，乙到達N點．
(1)請說明甲、乙兩人到達O點前，MN與AB不可能平行．
(2)當t為何值時，△OMN∽△OBA？
(3)甲、乙兩人之間的距離為MN的長，設s＝MN2，求s與t之間的函數關系式，并求甲、乙兩人之間距離的最小值．
查看答案和解析>>
科目：初中數學 來源：2012屆江蘇省江陰初級中學九年級5月中考模擬數學試卷（帶解析） 題型：解答題
已知：如圖1，矩形ABCD中，AB＝6，BC＝8，E、F、G、H分別是AB、BC、CD、DA四條邊上的點（且不與各邊頂點重合），設m＝EF＋FG＋GH＋HE，探索m的取值范圍．
（1）如圖2，當E、F、G、H分別是AB、BC、CD、DA四邊中點時，m＝ ．
（2）為了解決這個問題，小貝同學采用軸對稱的方法，如圖3，將整個圖形以CD為對稱軸
翻折，接著再連續翻折兩次，從而找到解決問題的途徑，求得m的取值范圍．①請在圖3
中補全小貝同學翻折后的圖形；②請你根據①中的圖形，求出m的取值范圍，并簡要說明理
由．
查看答案和解析>>
科目：初中數學 來源：2011年初中畢業升學考試（天津卷）數學 題型：解答題
（本題滿分14分，第（1）小題滿分4分，第（2）、（3）小題滿分各5分）在Rt△ABC中，∠ACB＝90°，BC＝30，AB＝50．點P是AB邊上任意一點，直線PE⊥AB，與邊AC或BC相交于E．點M在線段AP上，點N在線段BP上，EM＝EN，
．
（1）如圖1，當點E與點C重合時，求CM的長；
（2）如圖2，當點E在邊AC上時，點E不與點A、C重合，設AP＝x，BN＝y，求y關于x的函數關系式，并寫出函數的定義域；
（3）若△AME∽△ENB（△AME的頂點A、M
、E分別與△ENB的頂點E、N、B對應），求AP的
長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
