
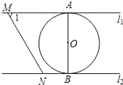
【題目】如圖,直線![]() ∥
∥![]() ,⊙O與
,⊙O與![]() 和
和![]() 分別相切于點A和點B.點M和點N分別是
分別相切于點A和點B.點M和點N分別是![]() 和
和![]() 上的動點,MN沿
上的動點,MN沿![]() 和
和![]() 平移.⊙O的半徑為1,∠1=60°.下列結論錯誤的是( )
平移.⊙O的半徑為1,∠1=60°.下列結論錯誤的是( )
A. ![]() B. l1和l2的距離為2
B. l1和l2的距離為2
C. 若∠MON=90°,則MN與⊙O相切 D. 若MN與⊙O相切,則![]()
【答案】D
【解析】
首先過點N作NC⊥AM于點C,直線l1∥l2,⊙O與l1和l2分別相切于點A和點B,⊙O的半徑為1,易求得MN=![]() =
=![]() ,l1和l2的距離為2;
,l1和l2的距離為2;
若∠MON=90°,連接NO并延長交MA于點C,易證得CO=NO,繼而可得即O到MN的距離等于半徑,可證得MN與⊙O相切;
由題意可求得若MN與⊙O相切,則AM=![]() 或
或![]() .
.
解:如圖1,過點N作NC⊥AM于點C,
∵直線l1∥l2,⊙O與l1和l2分別相切于點A和點B,⊙O的半徑為1,
∴CN=AB=2,
∵∠1=60°,
∴MN=![]() =
=![]() ,
,
故A與B正確;
如圖3,
若∠MON=90°,連接NO并延長交MA于點C,則△AOC≌△BON,
故CO=NO,△MON≌△MOM′,故MN上的高為1,即O到MN的距離等于半徑.
故C正確;
如圖2,∵MN是切線,⊙O與l1和l2分別相切于點A和點B,
∴∠AMO=![]() ∠1=30°,
∠1=30°,
∴AM=![]() ;
;
∵∠AM′O=60°,
∴AM′=![]() ,
,
∴若MN與⊙O相切,則AM=![]() 或
或![]() ;
;
故D錯誤.
故選:D.


科目:初中數學 來源: 題型:
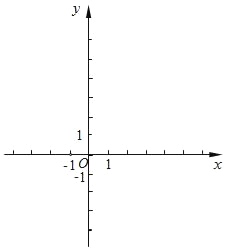
【題目】在平面直角坐標系xOy(如圖)中,拋物線y=ax2+bx+2經過點A(4,0)、B(2,2),與y軸的交點為C.
(1)試求這個拋物線的表達式;
(2)如果這個拋物線的頂點為M,求△AMC的面積;
(3)如果這個拋物線的對稱軸與直線BC交于點D,點E在線段AB上,且∠DOE=45°,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有一面12米長的墻,某農戶計劃用28米長的籬笆靠墻圍成一個矩形養雞場ABCD(籬笆只圍AB、BC、CD三邊),其示意圖如圖所示.
(1)若矩形養雞場的面積為92平方米,求所用的墻長AD.(結果精確到0.1米)(參考數據:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.24)
=2.24)
(2)求此矩形養雞場的最大面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
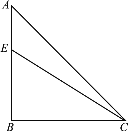
【題目】如圖,在Rt△ABC中,∠ABC=90°,AB=BC,點E為線段AB上一動點(不與點A,B重合),連接CE,將∠ACE的兩邊CE,CA分別繞點C順時針旋轉90°,得到射線CE,,CA,,過點A作AB的垂線AD,分別交射線CE,,CA,于點F,G.
(1)依題意補全圖形;
(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示);
(3)用等式表示線段AE,AF與BC之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個二次函數的對稱軸是x=1,圖象最低點P的縱坐標是﹣8,圖象過(﹣2,10)且與x軸交于A,B與y軸交于C.求:
(1)這個二次函數的解析式;
(2)△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
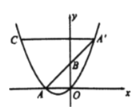
【題目】如圖,在平面直角坐標系中,拋物線![]() 交
交![]() 軸的負半軸于點
軸的負半軸于點![]() .點
.點![]() 是
是![]() 軸正半軸上一點,點
軸正半軸上一點,點![]() 關于點
關于點![]() 的對稱點
的對稱點![]() 恰好落在拋物線上.過點
恰好落在拋物線上.過點![]() 作
作![]() 軸的平行線交拋物線于另一點
軸的平行線交拋物線于另一點![]() .若點
.若點![]() 的橫坐標為1,則
的橫坐標為1,則![]() 的長為________.
的長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
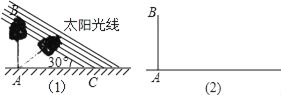
【題目】某數學興趣小組,利用樹影測量樹高,如圖(1),已測出樹AB的影長AC為12米,并測出此時太陽光線與地面成30°夾角.
(1)求出樹高AB;
(2)因水土流失,此時樹AB沿太陽光線方向倒下,在傾倒過程中,樹影長度發生了變化,假設太陽光線與地面夾角保持不變.求樹的最大影長.(用圖(2)解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
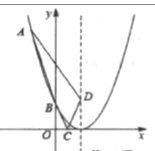
【題目】如圖,二次函數![]() 的圖像經過點
的圖像經過點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,![]() 、
、![]() 分別為
分別為![]() 軸、直線
軸、直線![]() 上的動點,當四邊形
上的動點,當四邊形![]() 的周長最小時,
的周長最小時,![]() 所在直線對應的函數表達式是( )
所在直線對應的函數表達式是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com