
【題目】今年某水果加工公司分兩次采購了一批桃子,第一次費用為25萬元,第二次費用為30萬元.已知第一次采購時每噸桃子的價格比去年的平均價格上漲了0.1萬元,第二次采購時每噸桃子的價格比去年的平均價格下降了0.1萬元,第二次采購的數量是第一次采購數量的2倍.
(1)試問去年每噸桃子的平均價格是多少萬元?兩次采購的總數量是多少噸?
(2)該公司可將桃子加工成桃脯或桃汁,每天只能加工其中一種.若單獨加工成桃脯,每天可加工3噸桃子,每噸可獲利0.7萬元;若單獨加工成桃汁,每天可加工9噸桃子,每噸可獲利0.2萬元.為出口需要,所有采購的桃子必須在30天內加工完畢.
①根據該公司的生產能力,加工桃脯的時間不能超過多少天?
②在這次加工生產過程中,應將多少噸桃子加工成桃脯才能獲取最大利潤?最大利潤為多少?
【答案】(1)去年每噸桃子的平均價格是0.4萬元/噸,兩次采購的總數量為150噸;(2)①加工桃脯的時間不能超過20天;②應將60噸桃子加工成桃脯才能獲取最大利潤,最大利潤為60萬元.
【解析】
(1)根據第二次采購的數量是第一次采購數量的2倍列方程即可求出去年每噸桃子的平均價格,然后再計算兩次采購的總數量;
(2)①根據所有采購的桃子必須在30天內加工完畢列出不等式求解即可;
②設該公司加工桃脯![]() 天,獲得最大利潤為
天,獲得最大利潤為![]() 萬元,根據題意列出
萬元,根據題意列出![]() 關于x的函數解析式,利用一次函數的性質求解即可.
關于x的函數解析式,利用一次函數的性質求解即可.
解:(1)設去年每噸桃子的平均價格是![]() 萬元/噸,
萬元/噸,
依題意,得:![]() ,
,
解得:![]() ,
,
經檢驗,![]() 是原方程的解,
是原方程的解,
![]() (噸),
(噸),
答:去年每噸桃子的平均價格是0.4萬元/噸,兩次采購的總數量為150噸;
(2)①設該公司加工桃脯用![]() 天,
天,
則![]() ,
,
解得:![]() ,
,
所以加工桃脯的時間不能超過20天;
②設該公司加工桃脯![]() 天,獲得最大利潤為
天,獲得最大利潤為![]() 萬元,
萬元,
依題意,得![]() ,
,
∵![]() ,
,
∴![]() 隨
隨![]() 的增大而增大,
的增大而增大,
∵![]() ,
,
∴當![]() 時,
時,![]() (萬元),
(萬元),
∴![]() (噸),
(噸),
答:應將60噸桃子加工成桃脯才能獲取最大利潤,最大利潤為60萬元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在![]() 中,點
中,點![]() ,
,![]() ,
,![]() 依次是邊
依次是邊![]() 的四等分點,點
的四等分點,點![]() ,
,![]() ,
,![]() 依次是邊
依次是邊![]() 的四等分點,分別以
的四等分點,分別以![]() ,
,![]() ,
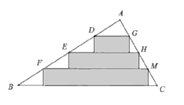
,![]() 為邊向下剪三個寬相等的矩形,如圖所示.若圖中空白部分的面積和為
為邊向下剪三個寬相等的矩形,如圖所示.若圖中空白部分的面積和為![]() ,則圖中陰影部分的面積和是( )
,則圖中陰影部分的面積和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(a<0)與x軸交于點A(﹣1,0),與y軸的交點在(0,2),(0,3)之間(包含端點),頂點坐標為(1,n),則下列結論:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③對于任意實數m,a+b≥am2+bm總成立;
④關于x的方程ax2+bx+c=n﹣1有兩個不相等的實數根.
其中結論正確的個數為( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
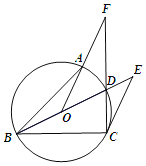
【題目】已知,如圖,BD為⊙O的直徑,點A、C在⊙O上并位于BD的兩側,∠ABC=45°,連結CD、OA并延長交于點F,過點C作⊙O的切線交BD延長線于點E.
(1)求證:∠F=∠ECF;
(2)當DF=6,tan∠EBC=![]() ,求AF的值.
,求AF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校團委準備暑期組織一次“研學之旅”活動,現有四個“研學”地方可選擇:井岡山、龍虎山、廬山、瑞金(其中井岡山、瑞金是紅色旅游勝地).校團委決定通過抽簽方式確定其中兩個地方.
抽簽規則:將四個地方分別寫在4張完全相同的紙牌正面,把4張紙牌背面朝上,洗勻后放在桌面上,團委書記小明先從中隨機抽取一張紙牌,記下地名,再從剩下的紙牌中隨機抽取第二張,記下地名.
(1)下列說法中,正確的序號是______.
①第一次“抽中井岡山”的概率是![]() ;
;
②“抽中的是兩個地方是紅色旅游勝地”是必然事件;
③“抽中的是兩個地方是紅色旅游勝地”是隨機事件;
④“抽中的是兩個地方是紅色旅游勝地”是不可能事件.
(2)用樹狀圖(或列表法)表示兩次抽牌所有可能出現的結果,并求“抽中的是兩個地方是紅色旅游勝地”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學的一個數學興趣小組在本校學生中開展了主題為“霧霾知多少”的專題調查括動,采取隨機抽樣的方式進行問卷調查,問卷調查的結果分為“A.非常了解”、“B.比較了解”、“C.基本了解”、“D.不太了解”四個等級,將所得數據進行整理后,繪制成如下兩幅不完整的統計圖表,請你結合圖表中的信息解答下列問題
等級 | A | B | C | D |
頻數 | 40 | 120 | 36 | n |
頻率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形統計圖中,A部分所對應的扇形的圓心角是 °,所抽取學生對丁霧霾了解程度的眾數是 ;
(3)若該校共有學生1500人,請根據調查結果估計這些學生中“比較了解”人數約為多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,函數
中,函數![]() 的圖象與直線
的圖象與直線![]() 交于點A(3,m).
交于點A(3,m).
(1)求k、m的值;
(2)已知點P(n,n)(n>0),過點P作平行于![]() 軸的直線,交直線y=x-2于點M,過點P作平行于y軸的直線,交函數
軸的直線,交直線y=x-2于點M,過點P作平行于y軸的直線,交函數![]() 的圖象于點N.
的圖象于點N.
①當n=1時,判斷線段PM與PN的數量關系,并說明理由;
②若PN≥PM,結合函數的圖象,直接寫出n的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
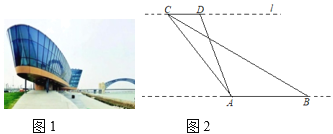
【題目】全國第二屆青年運動會是山西省歷史上第一次舉辦的大型綜合性運動會,太原作為主賽區,新建了很多場館,其中在汾河東岸落成了太原水上運動中心,它的終點塔及媒體中心是一個以“大帆船”造型(如圖1),外觀極具創新,這里主要承辦賽艇、皮劃艇、龍舟等項目的比賽.“青春”數學興趣小組為了測量“大帆船”AB的長度,他們站在汾河西岸,在與AB平行的直線l上取了兩個點C、D,測得CD=40m,∠CDA=120°,∠ACB=18.5°,∠BCD=26.5°,如圖2.請根據測量結果計算“大帆船”AB的長度.(結果精確到0.1m,參考數據:sin26.5°≈0.45,tan26.5°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
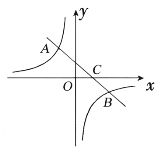
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于二、四象限內的
的圖象交于二、四象限內的![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,點
點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]()
(1)求該反比例函數和一次函數的解析式;
(2)連接![]() 、
、![]() ,求
,求![]() 的面積;
的面積;
(3)設點![]() 在
在![]() 軸上,且滿足
軸上,且滿足![]() 是直角三角形,直接寫出點
是直角三角形,直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com