
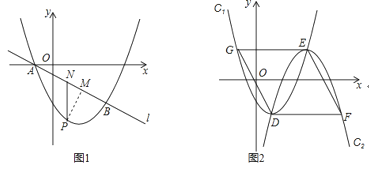
【題目】如圖1,拋物線![]() :
:![]() 與直線l:
與直線l:![]() 交于x軸上的一點(diǎn)A,和另一點(diǎn)
交于x軸上的一點(diǎn)A,和另一點(diǎn)![]()
![]() 求拋物線
求拋物線![]() 的解析式;
的解析式;
![]() 點(diǎn)P是拋物線
點(diǎn)P是拋物線![]() 上的一個(gè)動(dòng)點(diǎn)
上的一個(gè)動(dòng)點(diǎn)![]() 點(diǎn)P在A,B兩點(diǎn)之間,但不包括A,B兩點(diǎn)
點(diǎn)P在A,B兩點(diǎn)之間,但不包括A,B兩點(diǎn)![]() 于點(diǎn)M,
于點(diǎn)M,![]() 軸交AB于點(diǎn)N,求MN的最大值;
軸交AB于點(diǎn)N,求MN的最大值;
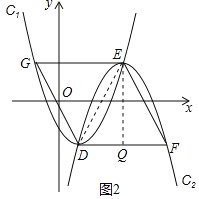
![]() 如圖2,將拋物線
如圖2,將拋物線![]() 繞頂點(diǎn)旋轉(zhuǎn)
繞頂點(diǎn)旋轉(zhuǎn)![]() 后,再作適當(dāng)平移得到拋物線
后,再作適當(dāng)平移得到拋物線![]() ,已知拋物線
,已知拋物線![]() 的頂點(diǎn)E在第一象限的拋物線
的頂點(diǎn)E在第一象限的拋物線![]() 上,且拋持線
上,且拋持線![]() 與拋物線
與拋物線![]() 交于點(diǎn)D,過點(diǎn)D作
交于點(diǎn)D,過點(diǎn)D作![]() 軸交拋物線
軸交拋物線![]() 于點(diǎn)F,過點(diǎn)E作
于點(diǎn)F,過點(diǎn)E作![]() 軸交拋物線
軸交拋物線![]() 于點(diǎn)G,是否存在這樣的拋物線
于點(diǎn)G,是否存在這樣的拋物線![]() ,使得四邊形DFEG為菱形?若存在,請(qǐng)求E點(diǎn)的橫坐標(biāo);若不存在,請(qǐng)說明理由.
,使得四邊形DFEG為菱形?若存在,請(qǐng)求E點(diǎn)的橫坐標(biāo);若不存在,請(qǐng)說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 點(diǎn)的橫坐標(biāo)為
點(diǎn)的橫坐標(biāo)為![]() 時(shí),四邊形DFEG為菱形
時(shí),四邊形DFEG為菱形
【解析】
![]() 求直線l與x軸交點(diǎn)A坐標(biāo)、B坐標(biāo),用待定系數(shù)法求拋物線
求直線l與x軸交點(diǎn)A坐標(biāo)、B坐標(biāo),用待定系數(shù)法求拋物線![]() 的解析式.
的解析式.
![]() 延長(zhǎng)PN交x軸于點(diǎn)H,設(shè)點(diǎn)P橫坐標(biāo)為m,由
延長(zhǎng)PN交x軸于點(diǎn)H,設(shè)點(diǎn)P橫坐標(biāo)為m,由![]() 軸可得點(diǎn)N、H橫坐標(biāo)也為m,即能用m表示PN、NH、AH的長(zhǎng).由
軸可得點(diǎn)N、H橫坐標(biāo)也為m,即能用m表示PN、NH、AH的長(zhǎng).由![]() 及對(duì)頂角
及對(duì)頂角![]() 可得
可得![]() 發(fā)現(xiàn)在
發(fā)現(xiàn)在![]() 中,MN與PN比值即為
中,MN與PN比值即為![]() ,故先在
,故先在![]() 中求
中求![]() 的值,再代入
的值,再代入![]() ,即得到MN與m的函數(shù)關(guān)系式,配方即求得MN最大值.
,即得到MN與m的函數(shù)關(guān)系式,配方即求得MN最大值.
![]() 設(shè)點(diǎn)
設(shè)點(diǎn)![]() ,所以可設(shè)拋物線
,所以可設(shè)拋物線![]() 頂點(diǎn)式為
頂點(diǎn)式為![]() 令兩拋物線解析式
令兩拋物線解析式![]() 列得關(guān)于x的方程,解得兩拋物線的另一交點(diǎn)D即為拋物線
列得關(guān)于x的方程,解得兩拋物線的另一交點(diǎn)D即為拋物線![]() 的頂點(diǎn),故DG
的頂點(diǎn),故DG![]() ,且求得DF平行且等于GE,即四邊形DFEG首先一定是平行四邊形.由DFEG為菱形可得
,且求得DF平行且等于GE,即四邊形DFEG首先一定是平行四邊形.由DFEG為菱形可得![]() ,故此時(shí)
,故此時(shí)![]() 為等邊三角形.利用特殊三角函數(shù)值作為等量關(guān)系列方程,即求得e的值.
為等邊三角形.利用特殊三角函數(shù)值作為等量關(guān)系列方程,即求得e的值.
解:![]() 直線l:
直線l:![]() 交x軸于點(diǎn)A,
交x軸于點(diǎn)A,
![]() ,解得:
,解得:![]() ,
,
![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 在直線l上,
在直線l上,
![]() ,
,
![]() ,
,
![]() 拋物線
拋物線![]() :
:![]() 經(jīng)過點(diǎn)A、B,
經(jīng)過點(diǎn)A、B,
![]() ,
,
解得: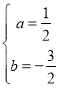 ,
,
![]() 拋物線
拋物線![]() 的解析式為
的解析式為![]() ,
,
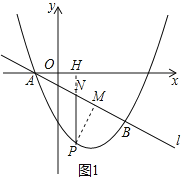
![]() 如圖1,延長(zhǎng)PN交x軸于點(diǎn)H,
如圖1,延長(zhǎng)PN交x軸于點(diǎn)H,
![]() ,
,
設(shè)![]() ,
,
![]() 軸,
軸,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,
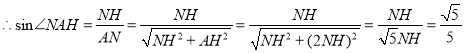 ,
,
![]() 于點(diǎn)M,
于點(diǎn)M,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() 的最大值為
的最大值為![]() ,
,
![]() 存在滿足條件的拋物線
存在滿足條件的拋物線![]() ,使得四邊形DFEG為菱形,
,使得四邊形DFEG為菱形,
如圖2,連接DE,過點(diǎn)E作![]() 于點(diǎn)Q,
于點(diǎn)Q,
![]() ,
,
![]() 拋物線
拋物線![]() 頂點(diǎn)為
頂點(diǎn)為![]() ,
,
設(shè)![]() ,
,
![]() 拋物線
拋物線![]() 頂點(diǎn)式為
頂點(diǎn)式為![]() ,
,
當(dāng)![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 兩拋物線另一交點(diǎn)
兩拋物線另一交點(diǎn)![]() 為拋物線
為拋物線![]() 頂點(diǎn),
頂點(diǎn),
![]() 軸,
軸,![]() 軸,
軸,
![]() ,
,![]() ,
,
![]() 四邊形DFEG是平行四邊形,
四邊形DFEG是平行四邊形,
若DFEG為菱形,則![]() ,
,
![]() 由拋物線對(duì)稱性可得:
由拋物線對(duì)稱性可得:![]() ,
,
![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]() ,
,
![]() ,
,
解得:![]() 舍去
舍去![]() ,
,![]() ,
,
![]() 點(diǎn)的橫坐標(biāo)為
點(diǎn)的橫坐標(biāo)為![]() 時(shí),四邊形DFEG為菱形.
時(shí),四邊形DFEG為菱形.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
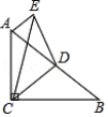
【題目】如圖,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是邊
是邊![]() 的中點(diǎn),連結(jié)
的中點(diǎn),連結(jié)![]() ,將
,將![]() 沿直線
沿直線![]() 翻折得到
翻折得到![]() ,連結(jié)
,連結(jié)![]() .若
.若![]() ,
,![]() ,則線段
,則線段![]() 的長(zhǎng)為( )
的長(zhǎng)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校為迎接縣中學(xué)生籃球比賽,計(jì)劃購買A、B兩種籃球共20個(gè)供學(xué)生訓(xùn)練使用.若購買A種籃球6個(gè),則購買兩種籃球共需費(fèi)用720元;若購買A種籃球12個(gè),則購實(shí)兩種籃球共需費(fèi)用840元.
(1)A、B兩種籃球共需單價(jià)各多少元?
(2)設(shè)購買A種籃球x個(gè)且A種籃球不少于8個(gè),所需費(fèi)用為y元,試確定y與x的關(guān)系式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
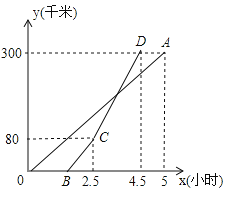
【題目】如圖:甲、乙兩地相距![]() ,一輛貨車和一輛轎車先后從甲地出發(fā)駛向乙地,線段
,一輛貨車和一輛轎車先后從甲地出發(fā)駛向乙地,線段![]() 和折線
和折線![]() 分別表示貨車和轎車離甲地的距離
分別表示貨車和轎車離甲地的距離![]()
![]() 與貨車出發(fā)時(shí)間
與貨車出發(fā)時(shí)間![]()
![]() 之間的函數(shù)關(guān)系,請(qǐng)根據(jù)圖象解答下列問題:
之間的函數(shù)關(guān)系,請(qǐng)根據(jù)圖象解答下列問題:
(1)貨車的速度為___________![]() ,當(dāng)轎車到達(dá)乙地后,貨車距乙地的距離為____________千米;
,當(dāng)轎車到達(dá)乙地后,貨車距乙地的距離為____________千米;
(2)求轎車改變速度后![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(3)轎車到達(dá)乙地后,馬上沿原路以![]() 段速度返回,求轎車從乙地出發(fā)后多長(zhǎng)時(shí)間再次與貨車相遇?
段速度返回,求轎車從乙地出發(fā)后多長(zhǎng)時(shí)間再次與貨車相遇?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
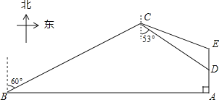
【題目】如圖,一般捕魚船在A處發(fā)出求救信號(hào),位于A處正西方向的B處有一艘救援艇決定前去數(shù)援,但兩船之間有大片暗礁,無法直線到達(dá).救援艇決定馬上調(diào)整方向,先向北偏東![]() 方以每小時(shí)30海里的速度航行,同時(shí)捕魚船向正北低速航行.30分鐘后,捕魚船到達(dá)距離A處
方以每小時(shí)30海里的速度航行,同時(shí)捕魚船向正北低速航行.30分鐘后,捕魚船到達(dá)距離A處![]() 海里的D處,此時(shí)救援艇在C處測(cè)得D處在南偏東
海里的D處,此時(shí)救援艇在C處測(cè)得D處在南偏東![]() 的方向上.
的方向上.
![]() 求C、D兩點(diǎn)的距離;
求C、D兩點(diǎn)的距離;
![]() 捕魚船繼續(xù)低速向北航行,救援艇決定再次調(diào)整航向,沿CE方向前去救援,并且捕魚船和救援艇同達(dá)時(shí)到E處,若兩船航速不變,求
捕魚船繼續(xù)低速向北航行,救援艇決定再次調(diào)整航向,沿CE方向前去救援,并且捕魚船和救援艇同達(dá)時(shí)到E處,若兩船航速不變,求![]() 的正弦值.
的正弦值.![]() 參考數(shù)據(jù):
參考數(shù)據(jù):![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
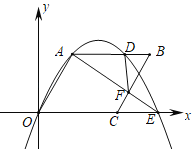
【題目】如圖,在平面直角坐標(biāo)系中,菱形OABC的邊長(zhǎng)為2,∠AOC=60°,點(diǎn)D為AB邊上的一點(diǎn),經(jīng)過O,A,D三點(diǎn)的拋物線與x軸的正半軸交于點(diǎn)E,連結(jié)AE交BC于點(diǎn)F,當(dāng)DF⊥AB時(shí),CE的長(zhǎng)為__.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
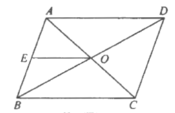
【題目】如圖,![]() 的周長(zhǎng)為36 cm,對(duì)角線
的周長(zhǎng)為36 cm,對(duì)角線![]() 相交于點(diǎn)
相交于點(diǎn)![]() cm.若點(diǎn)
cm.若點(diǎn)![]() 是
是![]() 的中點(diǎn),則
的中點(diǎn),則![]() 的周長(zhǎng)為( )
的周長(zhǎng)為( )
A.10 cmB.15 cmC.20 cmD.30 cm
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=∠ACB,以AC為直徑的⊙O分別交AB、BC于點(diǎn)M、N,點(diǎn)P在AB的延長(zhǎng)線上,且∠CAB=2∠BCP.
(1)求證:直線CP是⊙O的切線.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求點(diǎn)B到AC的距離.
,求點(diǎn)B到AC的距離.
(3)在第(2)的條件下,求△ACP的周長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
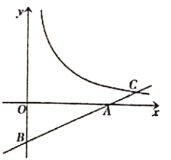
【題目】如圖,在平面直角坐標(biāo)系中,直線![]() 與
與![]() 軸,
軸,![]() 軸分別相交于
軸分別相交于![]() ,
,![]() 兩點(diǎn),與反比例函數(shù)
兩點(diǎn),與反比例函數(shù)![]() 的圖象交于點(diǎn)
的圖象交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 的橫坐標(biāo)為4.
的橫坐標(biāo)為4.
(1)求![]() 的值;
的值;
(2)過點(diǎn)![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,點(diǎn)
,點(diǎn)![]() 是該反比例函數(shù)
是該反比例函數(shù)![]() 的圖象上一點(diǎn),連接
的圖象上一點(diǎn),連接![]() ,
,![]() ,且
,且![]() .
.
①求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②求點(diǎn)![]() 到直線
到直線![]() 的距離
的距離![]() 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com