
【題目】閱讀下面的情景對話,然后解答問題: 
(1)根據“奇異三角形”的定義,請你判斷小華提出的命題:“等邊三角形一定是奇異三角形”是真命題還是假命題?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇異三角形,求a:b:c;
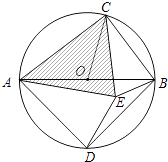
(3)如圖,AB是⊙O的直徑,C是⊙O上一點(不與點A、B重合),D是半圓 ![]() 的中點,C、D在直徑AB的兩側,若在⊙O內存在點E,使AE=AD,CB=CE. ①求證:△ACE是奇異三角形;
的中點,C、D在直徑AB的兩側,若在⊙O內存在點E,使AE=AD,CB=CE. ①求證:△ACE是奇異三角形;
②當△ACE是直角三角形時,求∠AOC的度數.
【答案】
(1)解:設等邊三角形的一邊為a,則a2+a2=2a2,
∴符合奇異三角形”的定義.
∴是真命題
(2)解:∵∠C=90°,
則a2+b2=c2①,
∵Rt△ABC是奇異三角形,且b>a,
∴a2+c2=2b2②,
由①②得:b= ![]() a,c=
a,c= ![]() a,
a,
∴a:b:c=1: ![]() :
: ![]()
(3)解:∵①AB是⊙O的直徑,
∴∠ACB=∠ADB=90°,
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2,
∵點D是半圓 ![]() 的中點,
的中點,
∴ ![]() =
= ![]() ,
,
∴AD=BD,
∴AB2=AD2+BD2=2AD2,
∴AC2+CB2=2AD2,
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2,
∴△ACE是奇異三角形;
②由①可得△ACE是奇異三角形,
∴AC2+CE2=2AE2,
當△ACE是直角三角形時,
由(2)得:AC:AE:CE=1: ![]() :
: ![]() 或AC:AE:CE=
或AC:AE:CE= ![]() :
: ![]() :1,
:1,
當AC:AE:CE=1: ![]() :
: ![]() 時,AC:CE=1:
時,AC:CE=1: ![]() ,即AC:CB=1:
,即AC:CB=1: ![]() ,
,
∵∠ACB=90°,
∴∠ABC=30°,
∴∠AOC=2∠ABC=60°;
當AC:AE:CE= ![]() :
: ![]() :1時,AC:CE=
:1時,AC:CE= ![]() :1,即AC:CB=
:1,即AC:CB= ![]() :1,
:1,
∵∠ACB=90°,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°.
∴∠AOC的度數為60°或120°.
【解析】(1)根據“奇異三角形”的定義與等邊三角形的性質,求證即可;(2)根據勾股定理與奇異三角形的性質,可得a2+b2=c2與a2+c2=2b2 , 用a表示出b與c,即可求得答案;(3)①AB是⊙O的直徑,即可求得∠ACB=∠ADB=90°,然后利用勾股定理與圓的性質即可證得;②利用(2)中的結論,分別從AC:AE:CE=1: ![]() :
: ![]() 與AC:AE:CE=
與AC:AE:CE= ![]() :
: ![]() :1去分析,即可求得結果.
:1去分析,即可求得結果.
【考點精析】掌握等邊三角形的性質和勾股定理的概念是解答本題的根本,需要知道等邊三角形的三個角都相等并且每個角都是60°;直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2.


 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
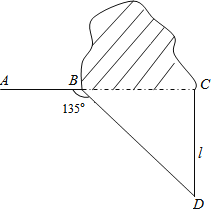
【題目】如圖,修公路遇到一座山,于是要修一條隧道.為了加快施工進度,想在小山的另一側同時施工.為了使山的另一側的開挖點C在AB的延長線上,設想過C點作直線AB的垂線L,過點B作一直線(在山的旁邊經過),與L相交于D點,經測量∠ABD=135°,BD=800米,求直線L上距離D點多遠的C處開挖?(![]() ≈1.414,精確到1米)
≈1.414,精確到1米)
查看答案和解析>>
科目:初中數學 來源: 題型:
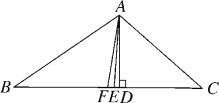
【題目】如圖,AE是△ABC的角平分線,AD⊥BC于點D,點F為BC的中點,若∠BAC=104°,∠C=40°,則有下列結論:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF=![]() S△ABC.其中正確的個數有( )
S△ABC.其中正確的個數有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①表示的是某綜合商場今年1~5月的商品各月銷售總額的情況,圖②表示的是商場服裝部各月銷售額占商場當月銷售總額的百分比情況,觀察圖①、圖②,解答下列問題: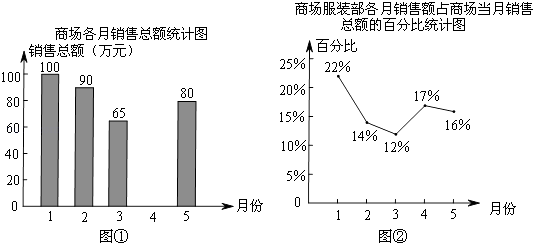
(1)來自商場財務部的數據報告表明,商場1~5月的商品銷售總額一共是410萬元,請你根據這一信息將圖①中的統計圖補充完整;
(2)商場服裝部5月份的銷售額是多少萬元?
(3)小剛觀察圖②后認為,5月份商場服裝部的銷售額比4月份減少了.你同意他的看法嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:(1)13=![]() ×12×22;(2)13+23=
×12×22;(2)13+23=![]() ×22×32;(3)13+23+33=
×22×32;(3)13+23+33=![]() ×32×42;(4)13+23+33+43=
×32×42;(4)13+23+33+43=![]() ×42×52;
×42×52;![]()
根據上述等式的規律,解答下列問題:
(1)寫出第5個等式:_____;
(2)寫出第n個等式(用含有n的代數式表示);
(3)設s是正整數且s≥2,應用你發現的規律,化簡:![]() ×s2×(s+1)2﹣
×s2×(s+1)2﹣![]() ×(s﹣1)2×s2.
×(s﹣1)2×s2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設A是由2×4個整數組成的2行4列的數表,如果某一行(或某一列)各數之和為負數,那么改變該行(或該列)中所有數的符號,稱為一次“操作”.
(1)如表1所示,如果經過兩次“操作”,使得到的數表每行的各數之和與每列的各數之和均為非負整數,請寫出每次“操作”后所得的數表;(寫出一種方法即可)
1 | 2 | 3 | -7 |
-2 | -1 | 0 | 1 |
表1
(2)如表2所示,若經過任意一次“操作”以后,便可使得到的數表每行的各數之和與每列的各數之和均為非負整數,求整數a的值.
a | a2-1 | -a | -a2 |
2-a | 1-a2 | a-2 | a2 |
表2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BA1和CA1分別是△ABC的內角平分線和外角平分線,BA2是∠A1BD的平分線,CA2是∠A1CD的平分線,BA3是∠A2BD的平分線,CA3是∠A2CD的平分線.若∠A1=α,則∠A2019=________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】媽媽要榨果汁,她有蘋果、橙子、雪梨三種水果,且其顆數比為 9:7:6, 她榨完果汁后,蘋果、橙子、雪梨的顆數比變為 6:3:4,已知媽媽榨果汁時沒有使用雪梨, 小明根據他的發現利用所學的數學知識推斷出媽媽榨果汁時只使用了橙子,媽媽告訴小明他的推斷是完全正確的。請你嘗試寫出小明的推斷過程。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線 l1 經過點 A(5,0)和點 B(![]() ,﹣5)
,﹣5)
(1)求直線 l1 的表達式;
(2)設直線 l2 的解析式為 y=﹣2x+2,且 l2 與 x 軸交于點 D,直線 l1 交 l2 于點 C, 求△CAD 的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com