
【題目】如圖,BA1和CA1分別是△ABC的內(nèi)角平分線和外角平分線,BA2是∠A1BD的平分線,CA2是∠A1CD的平分線,BA3是∠A2BD的平分線,CA3是∠A2CD的平分線.若∠A1=α,則∠A2019=________.


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,下列條件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4-∠1=180°中能判斷直線![]() ∥
∥![]() 的有( )
的有( )
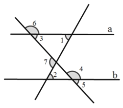
A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D、E是△ABC內(nèi)兩點(diǎn),AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,則BC= . 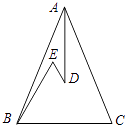
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下面的情景對話,然后解答問題: 
(1)根據(jù)“奇異三角形”的定義,請你判斷小華提出的命題:“等邊三角形一定是奇異三角形”是真命題還是假命題?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇異三角形,求a:b:c;
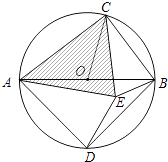
(3)如圖,AB是⊙O的直徑,C是⊙O上一點(diǎn)(不與點(diǎn)A、B重合),D是半圓 ![]() 的中點(diǎn),C、D在直徑AB的兩側(cè),若在⊙O內(nèi)存在點(diǎn)E,使AE=AD,CB=CE. ①求證:△ACE是奇異三角形;
的中點(diǎn),C、D在直徑AB的兩側(cè),若在⊙O內(nèi)存在點(diǎn)E,使AE=AD,CB=CE. ①求證:△ACE是奇異三角形;
②當(dāng)△ACE是直角三角形時,求∠AOC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將一塊直角三角板OAB放在平面直角坐標(biāo)系中,B(2,0),∠AOB=60°,點(diǎn)A在第一象限,過點(diǎn)A的雙曲線為 ![]() .在x軸上取一點(diǎn)P,過點(diǎn)P作直線OA的垂線l,以直線l為對稱軸,線段OB經(jīng)軸對稱變換后的像是O′B′.
.在x軸上取一點(diǎn)P,過點(diǎn)P作直線OA的垂線l,以直線l為對稱軸,線段OB經(jīng)軸對稱變換后的像是O′B′. 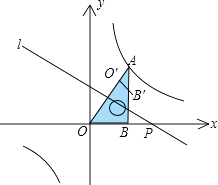
(1)當(dāng)點(diǎn)O′與點(diǎn)A重合時,點(diǎn)P的坐標(biāo)是;
(2)設(shè)P(t,0),當(dāng)O′B′與雙曲線有交點(diǎn)時,t的取值范圍是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某班師生組織植樹活動,上午8時從學(xué)校出發(fā),到植樹地點(diǎn)植樹后原路返校,如圖為師生離校路程s與時間t之間的圖象.請回答下列問題: 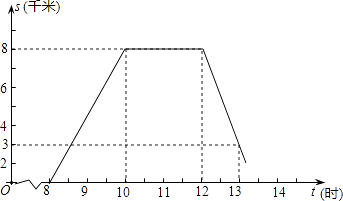
(1)求師生何時回到學(xué)校?
(2)如果運(yùn)送樹苗的三輪車比師生遲半小時出發(fā),與師生同路勻速前進(jìn),早半小時到達(dá)植樹地點(diǎn),請?jiān)趫D中,畫出該三輪車運(yùn)送樹苗時,離校路程s與時間t之間的圖象,并結(jié)合圖象直接寫出三輪車追上師生時,離學(xué)校的路程;
(3)如果師生騎自行車上午8時出發(fā),到植樹地點(diǎn)后,植樹需2小時,要求14時前返回到學(xué)校,往返平均速度分別為每時10km、8km.現(xiàn)有A、B、C、D四個植樹點(diǎn)與學(xué)校的路程分別是13km、15km、17km、19km,試通過計(jì)算說明哪幾個植樹點(diǎn)符合要求.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
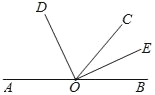
【題目】如圖,點(diǎn) A,O,B 在同一條直線上,OD,OE 分別平分∠AOC 和∠BOC.
(1)求∠DOE 的度數(shù);
(2)如果∠COD=65°,求∠AOE 的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在△ABC中,點(diǎn)O是AC上的一個動點(diǎn),過點(diǎn)O作直線MN∥BC,設(shè)MN交∠BCA的平分線于E,交∠BCA的外角平分線于F.
(1)請猜測OE與OF的大小關(guān)系,并說明你的理由;
(2)點(diǎn)O運(yùn)動到何處時,四邊形AECF是矩形?寫出推理過程;
(3)點(diǎn)O運(yùn)動到何處且△ABC滿足什么條件時,四邊形AECF是正方形?(寫出結(jié)論即可)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】完成下面的說理過程.
已知:如圖,OA=OB,AC=BC.

試說明:∠AOC=∠BOC.
解:在△AOC和△BOC中,
因?yàn)?/span>OA=______,AC=______,OC=______,
所以________≌________(SSS),
所以∠AOC=∠BOC(__________________).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com