
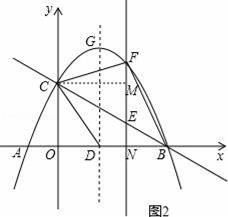
如圖,拋物線y=﹣
 x2+mx+n與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
x2+mx+n與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
(1)求拋物線的表達式;
(2)在拋物線的對稱軸上是否存在點P,使△PCD是以CD為腰的等腰三角形?如果存在,直接寫出P點的坐標;如果不存在,請說明理由;
(3)點E是線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時,四邊形CDBF的面積最大?求出四邊形CDBF的最大面積及此時E點的坐標.


【考點】二次函數綜合題.
【專題】代數幾何綜合題;壓軸題.
【分析】(1)由待定系數法建立二元一次方程組求出求出m、n的值即可;
(2)由(1)的解析式求出頂點坐標,再由勾股定理求出CD的值,再以點C為圓心,CD為半徑作弧交對稱軸于P1,以點D為圓心CD為半徑作圓交對稱軸于點P2,P3,作CE垂直于對稱軸與點E,由等腰三角形的性質及勾股定理就可以求出結論;
(3)先求出BC的解析式,設出E點的坐標為(a,﹣
 a+2),就可以表示出F的坐標,由四邊形CDBF的面積=S△BCD+S△CEF+S△BEF求出S與a的關系式,由二次函數的性質就可以求出結論.
a+2),就可以表示出F的坐標,由四邊形CDBF的面積=S△BCD+S△CEF+S△BEF求出S與a的關系式,由二次函數的性質就可以求出結論.
【解答】解:(1)∵拋物線y=﹣
 x2+mx+n經過A(﹣1,0),C(0,2).
x2+mx+n經過A(﹣1,0),C(0,2).
解得: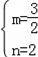
 ,
,
∴拋物線的解析式為:y=﹣
 x2+
x2+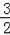
 x+2;
x+2;
(2)∵y=﹣
 x2+
x2+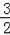
 x+2,
x+2,
∴y=﹣
 (x﹣
(x﹣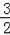
 )2+
)2+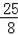
 ,
,
∴拋物線的對稱軸是x=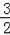
 .
.
∴OD=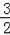
 .
.
∵C(0,2),
∴OC=2.
在Rt△OCD中,由勾股定理,得
CD=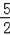
 .
.
∵△CDP是以CD為腰的等腰三角形,
∴CP1=DP2=DP3=CD.
作CM⊥x對稱軸于M,
∴MP1=MD=2,
∴DP1=4.
∴P1(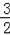
 ,4),P2(
,4),P2(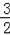
 ,
,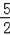
 ),P3(
),P3(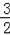
 ,﹣
,﹣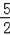
 );
);
(3)當y=0時,0=﹣
 x2+
x2+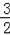
 x+2
x+2
∴x1=﹣1,x2=4,
∴B(4,0).
設直線BC的解析式為y=kx+b,由圖象,得
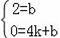
 ,
,
解得:
 ,
,
∴直線BC的解析式為:y=﹣
 x+2.
x+2.
如圖2,過點C作CM⊥EF于M,設E(a,﹣
 a+2),F(a,﹣
a+2),F(a,﹣
 a2+
a2+
 a+2),
a+2),
∴EF=﹣
 a2+
a2+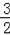
 a+2﹣(﹣
a+2﹣(﹣
 a+2)=﹣
a+2)=﹣
 a2+2a(0≤a≤4).
a2+2a(0≤a≤4).
∵S四邊形CDBF=S△BCD+S△CEF+S△BEF=
 BD•OC+
BD•OC+
 EF•CM+
EF•CM+
 EF•BN,
EF•BN,
=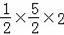
 +
+
 a(﹣
a(﹣
 a2+2a)+
a2+2a)+
 (4﹣a)(﹣
(4﹣a)(﹣
 a2+2a),
a2+2a),
=﹣a2+4a+
 (0≤a≤4).
(0≤a≤4).
=﹣(a﹣2)2+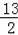

∴a=2時,S四邊形CDBF的面積最大=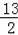
 ,
,
∴E(2,1).



【點評】本題考查了待定系數法求一次函數的解析式的運用,二次函數的解析式的運用,勾股定理的運用,等腰三角形的性質的運用,四邊形的面積的運用,解答時求出函數的解析式是關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
某家電集團公司研制生產的新家電,前期投資200萬元,每生產一臺這種新家電,后期還需投資0.3萬元。已知每臺新家電售價為0.5萬元。設總投資為P萬元,總利潤為Q萬元(總利潤=總產值-總投資),新家電總產量為x臺。(假設可按售價全部賣出)
(1)試用x的代數式表示P和Q;
(2)當總產量達到900臺時,該公司能否盈利?
(3)當總產量達到多少臺時,該公司開始盈利?
查看答案和解析>>
科目:初中數學 來源: 題型:
某超市銷售一種飲料,平均每天可售出100箱,每箱利潤120元。天氣漸熱,為了擴大
銷售,增加利潤,超市準備適當降價。據測算,若每箱飲料每降價1元,每天可多售出2箱。針對這種飲料的銷售情況,請解答以下問題:
(1)當每箱飲料降價20元時,這種飲料每天銷售獲利多少元?
(2)在要求每箱飲料獲利大于80元的情況下,要使每天銷售飲料獲利14400元,
問每箱應降價多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com