
【題目】已知:如圖,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,點E在邊AD上(不與點A、D重合),∠CEB=45°,EB與對角線AC相交于點F,設DE=x.
(1)用含x的代數式表示線段CF的長;
(2)如果把△CAE的周長記作C△CAE,△BAF的周長記作C△BAF,設![]() =y,求y關于x的函數關系式,并寫出它的定義域;
=y,求y關于x的函數關系式,并寫出它的定義域;
(3)當∠ABE的正切值是![]() 時,求AB的長.
時,求AB的長.

【答案】(1)![]() ;(2)y=
;(2)y=![]() (0<x<2),(3)
(0<x<2),(3)![]() .
.
【解析】試題分析:(1)根據等腰直角三角形的性質,求得∠DAC=∠ACD=45°,進而根據兩角對應相等的兩三角形相似,可得△CEF∽△CAE,然后根據相似三角形的性質和勾股定理可求解;
(2)根據相似三角形的判定與性質,由三角形的周長比可求解;
(3)由(2)中的相似三角形的對應邊成比例,可求出AB的關系,然后可由∠ABE的正切值求解.
試題解析:(1)∵AD=CD.
∴∠DAC=∠ACD=45°,
∵∠CEB=45°,
∴∠DAC=∠CEB,
∵∠ECA=∠ECA,
∴△CEF∽△CAE,
∴![]() ,
,
在Rt△CDE中,根據勾股定理得,CE=![]() ,
,
∵CA=2![]() ,
,
∴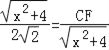 ,
,
∴CF=![]() ;
;
(2)∵∠CFE=∠BFA,∠CEB=∠CAB,
∴∠ECA=180°﹣∠CEB﹣∠CFE=180°﹣∠CAB﹣∠BFA,
∵∠ABF=180°﹣∠CAB﹣∠AFB,
∴∠ECA=∠ABF,
∵∠CAE=∠ABF=45°,
∴△CEA∽△BFA,
∴y=![]() =
=![]() =
=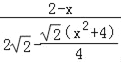 =
=![]() (0<x<2),
(0<x<2),
(3)由(2)知,△CEA∽△BFA,
∴![]() ,
,
∴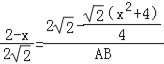 ,
,
∴AB=x+2,
∵∠ABE的正切值是![]() ,
,
∴tan∠ABE=![]() =
=![]() =
=![]() ,
,
∴x=![]() ,
,
∴AB=x+2=![]() .
.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數學 來源: 題型:
【題目】王老漢為了與顧客簽訂購銷合同,對自己魚塘中魚的總質量進行了估計,第一次撈出100條,稱得質量為184千克.并將每條魚做上記號后放入水中,當它們完全混合于魚群后,又撈出200條,稱得質量為416千克,且帶有記號的魚有20條,王老漢的魚塘中估計有魚多少條魚?總質量為多少千克?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學生小明、小華為了解本校八年級學生每周上網的時間,各自進行了抽樣調查.小明調查了八年級信息技術興趣小組中40名學生每周上網的時間,算得這些學生平均每周上網時間為2.5h;小華從全體320名八年級學生名單中隨機抽取了40名學生,調查了他們每周上網的時間,算得這些學生平均每周上網時間為1.2h.小明與小華整理各自樣本數據,如表所示.
時間段(h/周) | 小明抽樣人數 | 小華抽樣人數 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每組可含最低值,不含最高值)
請根據上述信息,回答下列問題:
(1)你認為哪位學生抽取的樣本具有代表性?_____.
估計該校全體八年級學生平均每周上網時間為_____h;
(2)在具有代表性的樣本中,中位數所在的時間段是_____h/周;
(3)專家建議每周上網2h以上(含2h)的同學應適當減少上網的時間,根據具有代表性的樣本估計,該校全體八年級學生中有多少名學生應適當減少上網的時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們給出如下定義:若一個四邊形中存在相鄰兩邊的平方和等于一條對角線的平方,則稱這個四邊形為勾股四邊形,這兩條相鄰的邊稱為這個四邊形的勾股邊.
(1)寫出你所知道的四邊形中是勾股四邊形的兩種圖形的名稱_____,_____;
(2)如圖,將△ABC繞頂點B按順時針方向旋轉60°后得到△DBE,連接AD、DC,若∠DCB=30°,試證明;DC2+BC2=AC2.(即四邊形ABCD是勾股四邊形)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲,乙兩輛汽車分別從A,B兩地同時出發,沿同一條公路相向而行,乙車出發2h后休息,與甲車相遇后,繼續行駛.設甲、乙兩車與B地的路程分別為y甲(km),y乙(km),甲車行駛的時間為x(h),y甲,y乙與x之間的函數圖象如圖所示,結合圖象解答下列問題:
(1)乙車休息了 _________ h;
(2)求乙車與甲車相遇后y乙與x的函數解析式,并寫出自變量x的取值范圍;.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是△ABC的外接圓,O點在BC邊上,∠BAC的平分線交⊙O于點D,連接BD、CD,過點D作BC的平行線,與AB的延長線相交于點P.
(1)求證:PD是⊙O的切線;
(2)求證:△PBD∽△DCA;
(3)當AB=6,AC=8時,求線段PB的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了提高學生閱讀能力,我區某校倡議八年級學生利用雙休日加強課外閱讀,為了解同學們閱讀的情況,學校隨機抽查了部分同學周末閱讀時間,并且得到數據繪制了不完整的統計圖,根據圖中信息回答下列問題:
(1)將條形統計圖補充完整;被調查的學生周末閱讀時間眾數是多少小時,中位數是多少小時;
(2)計算被調查學生閱讀時間的平均數;
(3)該校八年級共有500人,試估計周末閱讀時間不低于1.5小時的人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某蘋果生產基地,用30名工人進行采摘或加工蘋果 ,每名工人只能做其中一項工作.蘋果的銷售方式有兩種:一種是可以直接出售;另一種是可以將采摘的蘋果加工成罐頭出售.直接出售每噸獲利4 000元;加工成罐頭出售每噸獲利10 000元.采摘的工人每人可采摘蘋果0.4噸;加工罐頭的工人每人可加工0.3噸.設有x名工人進行蘋果采摘,全部售出后,總利潤為y元.
(1)求y與x的函數關系式;
(2)如何分配工人才能獲利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com