
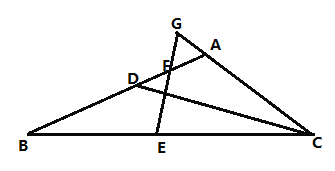
【題目】閱讀材料:如圖1,![]() 中,點(diǎn)
中,點(diǎn)![]() ,
,![]() 在邊
在邊![]() 上,點(diǎn)
上,點(diǎn)![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() ,延長(zhǎng)
,延長(zhǎng)![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() ,求證:
,求證:![]() .
.
等腰三角形是一種常見的軸對(duì)稱圖形,幾何試題中我們常將一腰所在的三角形沿著等腰三角形的對(duì)稱軸進(jìn)行翻折,從而構(gòu)造軸對(duì)稱圖形.
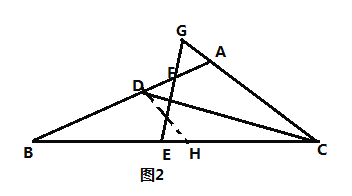
①小明的想法是:將![]() 放到
放到![]() 中,沿等腰
中,沿等腰![]() 的對(duì)稱軸進(jìn)行翻折,即作
的對(duì)稱軸進(jìn)行翻折,即作![]() 交
交![]() 于
于![]() (如圖2)
(如圖2)
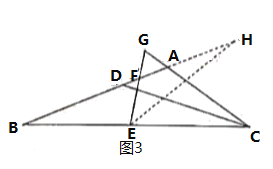
②小白的想法是:將![]() 放到
放到![]() 中,沿等腰
中,沿等腰![]() 的對(duì)稱軸進(jìn)行翻折,即作
的對(duì)稱軸進(jìn)行翻折,即作![]() 交
交![]() 的延長(zhǎng)線于
的延長(zhǎng)線于![]() (如圖3)
(如圖3)
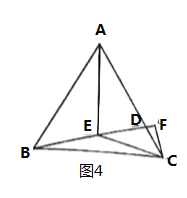
經(jīng)驗(yàn)拓展:等邊![]() 中,
中,![]() 是
是![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() ,
,![]() 為
為![]() 上一點(diǎn),
上一點(diǎn),![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 交
交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長(zhǎng)(用含
的長(zhǎng)(用含![]() ,
,![]() 的式子表示).
的式子表示).
【答案】①證明見解析;②證明見解析;[經(jīng)驗(yàn)拓展]![]() .
.
【解析】
閱讀材料:①先根據(jù)三角形全等的判定定理得出![]() ,再根據(jù)三角形全等的性質(zhì)可得
,再根據(jù)三角形全等的性質(zhì)可得![]() ,又根據(jù)角的和差、等腰三角形的性質(zhì)得出兩組相等的角
,又根據(jù)角的和差、等腰三角形的性質(zhì)得出兩組相等的角![]() ,然后根據(jù)三角形全等的判定定理與性質(zhì)可得
,然后根據(jù)三角形全等的判定定理與性質(zhì)可得![]() ,最后根據(jù)等量代換即可得證;
,最后根據(jù)等量代換即可得證;
②先根據(jù)三角形全等的判定定理得出![]() ,再根據(jù)三角形全等的性質(zhì)可得
,再根據(jù)三角形全等的性質(zhì)可得![]() ,又根據(jù)角的和差、等腰三角形的性質(zhì)得出兩組相等的角
,又根據(jù)角的和差、等腰三角形的性質(zhì)得出兩組相等的角![]() ,然后根據(jù)三角形全等的判定定理與性質(zhì)可得
,然后根據(jù)三角形全等的判定定理與性質(zhì)可得![]() ,即得證;
,即得證;
經(jīng)驗(yàn)拓展:先根據(jù)等腰三角形的性質(zhì)、鄰補(bǔ)角的定義得出![]() ,再根據(jù)三角形全等的判定定理與性質(zhì)得出
,再根據(jù)三角形全等的判定定理與性質(zhì)得出![]() ,設(shè)
,設(shè)![]() ,根據(jù)等腰三角形的性質(zhì)、等邊三角形的性質(zhì)分別求出
,根據(jù)等腰三角形的性質(zhì)、等邊三角形的性質(zhì)分別求出![]() ,然后根據(jù)角的和差可得
,然后根據(jù)角的和差可得![]() ,最后根據(jù)等腰三角形的判定與性質(zhì)得出
,最后根據(jù)等腰三角形的判定與性質(zhì)得出![]() ,從而根據(jù)線段的和差即可得出答案.
,從而根據(jù)線段的和差即可得出答案.
閱讀材料:
①小明做法:作![]() 交
交![]() 于
于![]() ,則
,則![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
![]() ;
;
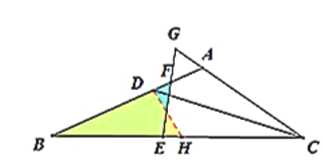
②小白做法:作![]() 交
交![]() 的延長(zhǎng)線于
的延長(zhǎng)線于![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]() ;
;

經(jīng)驗(yàn)拓展:延長(zhǎng)![]() 至點(diǎn)
至點(diǎn)![]() ,使得
,使得![]() ,連接
,連接![]()
![]()
![]()
![]()
![]()
![]()
![]() 是等邊三角形,設(shè)
是等邊三角形,設(shè)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 是等腰三角形
是等腰三角形
![]() (等腰三角形的三線合一)
(等腰三角形的三線合一)
![]() .
.



 小天才課時(shí)作業(yè)系列答案
小天才課時(shí)作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測(cè)驗(yàn)系列答案
黃岡小狀元滿分沖刺微測(cè)驗(yàn)系列答案 新輔教導(dǎo)學(xué)系列答案
新輔教導(dǎo)學(xué)系列答案 陽光同學(xué)一線名師全優(yōu)好卷系列答案
陽光同學(xué)一線名師全優(yōu)好卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,以AB上一點(diǎn)O為圓心,OA長(zhǎng)為半徑的圓恰好與BC相切于點(diǎn)D,分別交AC、AB于點(diǎn)E、F.
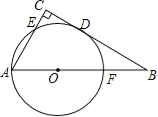
(1)若∠B=30°,求證:以A、O、D、E為頂點(diǎn)的四邊形是菱形.
(2)若AC=6,AB=10,連結(jié)AD,求⊙O的半徑和AD的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)![]() 中,正比例函數(shù)
中,正比例函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象經(jīng)過點(diǎn)
的圖象經(jīng)過點(diǎn)![]() .
.
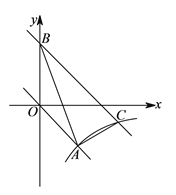
(![]() )分別求這兩個(gè)函數(shù)的表達(dá)式.
)分別求這兩個(gè)函數(shù)的表達(dá)式.
(![]() )將直線
)將直線![]() 向上平移
向上平移![]() 個(gè)單位長(zhǎng)度后與
個(gè)單位長(zhǎng)度后與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與反比例函數(shù)圖象在第四象限內(nèi)的交點(diǎn)為
,與反比例函數(shù)圖象在第四象限內(nèi)的交點(diǎn)為![]() ,連接
,連接![]() 、
、![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo)及
的坐標(biāo)及![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,PA、PB是⊙O的切線,A、B為切點(diǎn),∠APB=40°,點(diǎn)C是⊙O上不同于A、B的任意一點(diǎn),則∠ACB的度數(shù)為______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在⊙O中,AB為直徑,C為⊙O上一點(diǎn).

(1)如圖1,過點(diǎn)C作⊙O的切線,與AB延長(zhǎng)線相交于點(diǎn)P,若∠CAB=27°,求∠P的度數(shù);
(2)如圖2,D為弧AB上一點(diǎn),OD⊥AC,垂足為E,連接DC并延長(zhǎng),與AB的延長(zhǎng)線交于點(diǎn)P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在![]() 中,內(nèi)角
中,內(nèi)角![]() 與外角
與外角![]() 的平分線相交于點(diǎn)
的平分線相交于點(diǎn)![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,連接
,連接![]() 、
、![]() ,下列結(jié)論:①
,下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() 垂直平分
垂直平分![]() ;④
;④![]() .其中正確的是( )
.其中正確的是( )
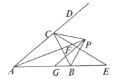
A. ①②④B. ①③④C. ②③④D. ①③
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
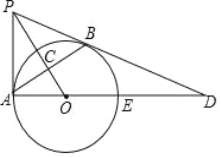
【題目】如圖,PB與⊙O相切于點(diǎn)B,過點(diǎn)B作OP的垂線BA,垂足為C,交⊙O于點(diǎn)A,連結(jié)PA,AO,AO的延長(zhǎng)線交⊙O于點(diǎn)E,與PB的延長(zhǎng)線交于點(diǎn)D.
(1)求證:PA是⊙O的切線;
(2)若tan∠BAD=![]() ,且OC=4,求BD的長(zhǎng).
,且OC=4,求BD的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
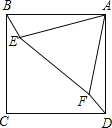
【題目】如圖,正方形ABCD與正三角形AEF的頂點(diǎn)A重合,將△AEF繞頂點(diǎn)A旋轉(zhuǎn),在旋轉(zhuǎn)過程中,當(dāng)BE=DF時(shí),∠BAE的大小可以是__.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在邊長(zhǎng)為1的小正方形組成的正方形網(wǎng)格中,建立如圖所示的平面真角坐標(biāo)系,已知格點(diǎn)三角形![]() (三角形的三個(gè)頂點(diǎn)都在格點(diǎn)上)
(三角形的三個(gè)頂點(diǎn)都在格點(diǎn)上)
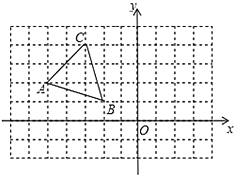
(1)畫出![]() 關(guān)于直線
關(guān)于直線![]() 對(duì)稱的
對(duì)稱的![]() ;并寫出點(diǎn)
;并寫出點(diǎn)![]() 、
、![]() 、
、![]() 的坐標(biāo).
的坐標(biāo).
(2)在直線![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使
,使![]() 最小,在圖中描出滿足條件的
最小,在圖中描出滿足條件的![]() 點(diǎn)(保留作圖痕跡),并寫出點(diǎn)
點(diǎn)(保留作圖痕跡),并寫出點(diǎn)![]() 的坐標(biāo)(提示:直線
的坐標(biāo)(提示:直線![]() 是過點(diǎn)
是過點(diǎn)![]() 且垂直于
且垂直于![]() 軸的直線)
軸的直線)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com