
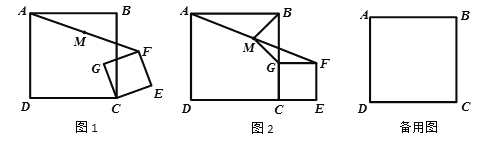
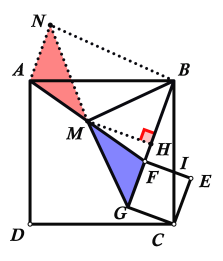
【題目】如圖1,正方形CEFG繞正方形ABCD的頂點C旋轉(zhuǎn),連接AF,點M是AF中點.
(1)當(dāng)點G在BC上時,如圖2,連接BM、MG,求證:BM=MG;
(2)在旋轉(zhuǎn)過程中,當(dāng)點B、G、F三點在同一直線上,若AB=5,CE=3,則MF= ;
(3)在旋轉(zhuǎn)過程中,當(dāng)點G在對角線AC上時,連接DG、MG,請你畫出圖形,探究DG、MG的數(shù)量關(guān)系,并說明理由.
【答案】(1)證明見解析;(2)![]() 或
或![]() ;(3)DG=
;(3)DG=![]() MG,理由見解析.
MG,理由見解析.
【解析】
(1)連接MG并延長交AB于N點,證明△ANM≌△FGM后得到MG=MN,AN=CG,進(jìn)而得到BN=BG,得到△ANG為等腰直角三角形,即可證明MG=MB.
(2)分兩種情況畫出圖形再利用(1)中的思路結(jié)合勾股定理即可求解.
(3)先畫出圖形,然后證明△ADG≌△ABG,得到DG=BG,又△BMG為等腰直角三角形,故而得到DG=BG=![]() MG.
MG.
解:(1) 連接MG并延長交AB于N點,如下圖所示:
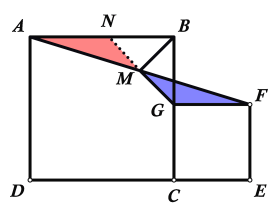
∵GF∥AN,
∴∠NAM=∠GFM
在△ANM和△FGM中
 ,∴△ANM≌△FGM(ASA)
,∴△ANM≌△FGM(ASA)
∴MG=MN,CG=GF=AN
∴AB-AN=BC-CG
∴NB=GB
∴△NBG為等腰直角三角形
又M是NG的中點
∴由直角三角形斜邊上的中線等于斜邊的一半知:
故有:MG=MB.
(2)分類討論:
情況一:當(dāng)B、G、F三點在正方形ABCD外同一直線上時

延長MG到N點,并使得MG=MN,連接AN,BN
∴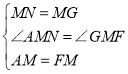 ,∴△AMN≌△FMG(SAS)
,∴△AMN≌△FMG(SAS)
∴AN=GF=GC,∠NAM=∠GFM
∴AN∥GF
∴∠NAB+∠ABG=180°
又∠ABC=90°
∴∠NAB+∠CBG=90°
又在△BCG中,∠BCG+∠CBG=90°
∴∠NAB=∠BCG
∴在△ABN中和△CBG中: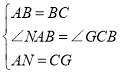 ,∴△ABN≌△CBG(SAS)
,∴△ABN≌△CBG(SAS)
∴BN=BG,∠ABN=∠CBG
∴∠ABC=∠NBG=90°
∴△NBG是等腰直角三角形,且∠BGN=45°
在Rt△BCG中,![]()
過M點作MH⊥BG于H點,∴△MHB為等腰直角三角形
∴MH=BH=HG=![]() BG=2
BG=2
在Rt△MFH中,![]()
情況二:當(dāng)B、G、F三點在正方形ABCD內(nèi)同一直線上時
如下圖所示,延長MG到MN,并使得MG=MN,連接NA、NB,
同情況一中證明思路,
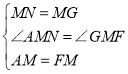 ,△AMN≌△FMG(SAS)
,△AMN≌△FMG(SAS)
∴AN=GF=GC,∠NAM=∠GFM
∴AN∥GF
∴∠NAB=∠ABG
又∠ABG+∠GBC=90°
∠GBC+∠BIF=90°
∴∠BIF=∠ABG
又∠BIF=∠BCG,∠ABC=∠NAB
∴∠NAB=∠GCB
∴在△ABN中和△CBG中: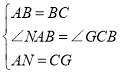 ,∴△ABN≌△CBG(SAS)
,∴△ABN≌△CBG(SAS)
∴BN=BG,∠ABN=∠CBG
∴∠ABC=∠NBG=90°
∴△NBG是等腰直角三角形,且∠BGN=45°
在△BCG中,![]()
過M點作MH⊥BG于H點,∴△MHB為等腰直角三角形
∴MH=BH=HG=![]() BG=2
BG=2
∴HF=HG-GF=2-1=1
在Rt△MFH中,![]()
故答案為:![]() 或
或![]()
(3)由題意作出圖形如下所示:
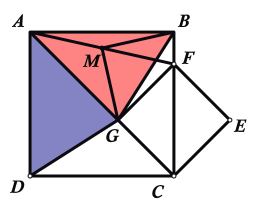
DG、MG的數(shù)量關(guān)系為:DG=![]() MG,理由如下:
MG,理由如下:
∵G點在AC上
∴∠DAG=∠BAG=45°
在△ADG和△ABG中:
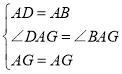 ,∴△ADG≌△BAG(SAS)
,∴△ADG≌△BAG(SAS)
∴DG=BG
又由(2)中的證明過程可知:△MBG為等腰直角三角形
∴BG=![]() MG
MG
∴DG=![]() MG
MG
故答案為:DG=![]() MG.
MG.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:初中數(shù)學(xué) 來源: 題型:
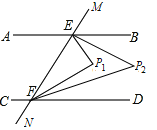
【題目】如圖,已知直線AB∥CD,MN分別交AB,CD于點E,F,∠BEF與∠DFE的兩條平分線相交于點P1,∠BEP1與∠DFP1的兩條平分線相交于點P2,則∠P2的度數(shù)為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在“宏揚傳統(tǒng)文化,打造書香校園”活動中,學(xué)校計劃開展四項活動:“A:國學(xué)誦讀”,“B:演講”,“C:課本劇”,“D:書法”.每位同學(xué)必須且只能參加其中一項活動,學(xué)校為了了解學(xué)生的意愿,隨機調(diào)查了部分學(xué)生,結(jié)果統(tǒng)計如圖所示:

(1) 此次一共抽取 名學(xué)生進(jìn)行統(tǒng)計調(diào)查;扇形統(tǒng)計圖中,活動D所占圓心角為 °;
(2) 請補全條形統(tǒng)計圖;
(3) 學(xué)校共有720名學(xué)生希望參加活動A,試估算該校共有多少名學(xué)生.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為預(yù)防疾病,某校對教室進(jìn)行“藥熏消毒”.已知藥物燃燒階段,室內(nèi)每立方米空氣中的含藥量![]() (mg)與燃燒時間
(mg)與燃燒時間![]() (分鐘)成正比例;燃燒后,
(分鐘)成正比例;燃燒后, ![]() 與
與![]() 成反比例(如圖所示).現(xiàn)測得藥物10分鐘燃完,此時教室內(nèi)每立方米空氣含藥量為8mg.據(jù)以上信息解答下列問題:
成反比例(如圖所示).現(xiàn)測得藥物10分鐘燃完,此時教室內(nèi)每立方米空氣含藥量為8mg.據(jù)以上信息解答下列問題:
(1)求藥物燃燒時![]() 與
與![]() 的函數(shù)關(guān)系式.(2)求藥物燃燒后
的函數(shù)關(guān)系式.(2)求藥物燃燒后![]() 與
與![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.
(3)當(dāng)每立方米空氣中含藥量低于1.6mg時,對人體方能無毒害作用,那么從消毒開始,經(jīng)多長時間學(xué)生才可以回教室?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一次函數(shù)![]() 的圖象經(jīng)過第一、二、三象限,且與反比例函數(shù)圖象相交于
的圖象經(jīng)過第一、二、三象限,且與反比例函數(shù)圖象相交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
, ![]() .且點
.且點![]() 橫坐標(biāo)是點
橫坐標(biāo)是點![]() 縱坐標(biāo)的2倍.
縱坐標(biāo)的2倍.
(1)求反比例函數(shù)的解析式;
(2)設(shè)點![]() 橫坐標(biāo)為
橫坐標(biāo)為![]() ,
, ![]() 面積為
面積為![]() ,
,
求![]() 與
與![]() 的函數(shù)關(guān)系式,并求出自變量的取值范圍.
的函數(shù)關(guān)系式,并求出自變量的取值范圍.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
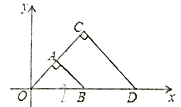
【題目】如圖,△OAB與△OCD是以點0為位似中心的位似圖形,相似比為1:2,∠OCD=90![]() ,CO=CD.若B(2,0),則點C的坐標(biāo)為( )
,CO=CD.若B(2,0),則點C的坐標(biāo)為( )
A. (2,2) B. (1,2) C. (![]() ,2
,2![]() ) D. (2,1)
) D. (2,1)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB⊥BC,AE平分∠BAD交BC于點E,AE⊥DE,∠1+∠2=90°,M、N分別是BA,CD延長線上的點,∠EAM和∠EDN的平分線交于點F,下列結(jié)論:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F為定值.其中結(jié)論正確的有( )

A. 4個B. 1個C. 2個D. 3個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
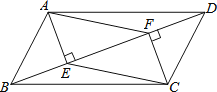
【題目】如圖,在平行四邊形ABCD中,AE⊥BD于E,CF⊥BD于F,連結(jié)AF,CE.求證:四邊形AECF是平行四邊形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB∥CD,∠BAC與∠DCA的平分線相交于點G,GE⊥AC于點E,F為AC上的一點,且AF=FC,GH⊥CD于H.下列說法①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH∶∠ECH=2∶7,則∠EGH=40°.其中正確的有________.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com