
【題目】如圖所示,⊙O是△ABC的外接圓,AB為直徑,∠BAC的平分線交⊙O于點D,過點D的切線分別交AB,AC的延長線于點E,F.
(1)求證:AF⊥EF.
(2)探究線段AF、CF、AB之間的數量關系,并證明.

【答案】(1)證明見解析;(2)AF+CF=AB.證明見解析.
【解析】
(1)連接OD,由EF是⊙O的切線,可得OD⊥EF,由∠BAC的平分線交⊙O與點D,易證得OD⊥BC,即可得BC∥EF,由AB為直徑,根據直徑所對的圓周角是直角,可得AC⊥BC,繼而證得AF⊥EF;
(2)連接BD并延長,交AF的延長線于點H,連接CD,易證得△ADH≌△ADB,△CDF≌△HDF,繼而證得AF+CF=AB.
(1)連接OD,
∴OD⊥EF,
∵AD平分∠BAC,
∴![]() ,
,
由垂徑定理知OD⊥BC,
又AB是直徑,
∴∠ACB=90°,即AF⊥BC,
∴AF∥OD,
∴AF⊥EF;
(2)AF+CF=AB,證明如下:
過D作DH⊥AB于H,則DH=DF,AH=AF,
∵![]() ,
,
∴DC=DB,
在 Rt△CFD與 Rt△BHD中,
![]() ,
,
∴Rt△CFD≌Rt△BHD(HL),
∴BH=CF,
∴AB=AH+HB=AF+CF.


科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 為
為![]() 邊上的一動點(
邊上的一動點(![]() 點不與
點不與![]() 、
、![]() 兩點重合).
兩點重合).![]() 交
交![]() 于
于![]() 點,
點,![]() 交
交![]() 于
于![]() 點.
點.

![]() 下列條件中:①
下列條件中:①![]() ;②
;②![]() 是
是![]() 的中線;③
的中線;③![]() 是
是![]() 的角平分線;④
的角平分線;④![]() 是
是![]() 的高,請選擇一個
的高,請選擇一個![]() 滿足的條件,使得四邊形
滿足的條件,使得四邊形![]() 為菱形,并證明;
為菱形,并證明;
答:我選擇________.(填序號)
![]() 在
在![]() 選擇的條件下,
選擇的條件下,![]() 再滿足條件:________,四邊形
再滿足條件:________,四邊形![]() 即成為正方形.
即成為正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知矩形![]() 和點
和點![]() ,當點
,當點![]() 在
在![]() 上任一位置(如圖
上任一位置(如圖![]() 所示)時,易證得結論:
所示)時,易證得結論:![]() ,請你探究:當點
,請你探究:當點![]() 分別在圖
分別在圖![]() 、圖
、圖![]() 中的位置時,
中的位置時,![]() 、
、![]() 、
、![]() 和
和![]() 又有怎樣的數量關系請你寫出對上述兩種情況的探究結論,并利用圖
又有怎樣的數量關系請你寫出對上述兩種情況的探究結論,并利用圖![]() 證明你的結論.
證明你的結論.
答:對圖![]() 的探究結論為________;
的探究結論為________;
對圖![]() 的探究結論為________;
的探究結論為________;
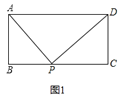


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() .
.

(1)先作![]() 的平分線交
的平分線交![]() 邊于點
邊于點![]() ,再以點
,再以點![]() 為圓心,
為圓心,![]() 長為半徑作⊙
長為半徑作⊙![]() .
.
(要求:尺規作圖,保留作圖痕跡,不寫作法)
(2)請你判斷(1)中![]() 與⊙
與⊙![]() 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
(3)若![]() ,
,![]() ,求出(1)中⊙
,求出(1)中⊙![]() 的半徑.
的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有下列說法:
①同一個人在相同的條件下做同一個實驗,第一天做了![]() 次,第二天做了
次,第二天做了![]() 次,對這一實驗中的同一事件來說,這兩天出現的頻率相等;
次,對這一實驗中的同一事件來說,這兩天出現的頻率相等;
②投擲骰子,偶數朝上的概率是![]() ;
;
③如果一個袋里裝有![]() 個紅球,
個紅球,![]() 個白球,從中任取
個白球,從中任取![]() 個,因為取出的球不是紅球,就是白球,所以取出紅球的概率是
個,因為取出的球不是紅球,就是白球,所以取出紅球的概率是![]() .
.
其中正確的有( )
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為一座拋物線型的拱橋,AB、CD分別表示兩個不同位置的水面寬度,O為拱橋頂部,水面AB寬為10米,AB距橋頂O的高度為12.5米,水面上升2.5米到達警戒水位CD位置時,水面寬為( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某批發門市銷售兩種商品,甲種商品每件售價為300元,乙種商品每件售價為80元.新年來臨之際,該門市為促銷制定了兩種優惠方案:
方案一:買一件甲種商品就贈送一件乙種商品;
方案二:按購買金額打八折付款.
某公司為獎勵員工,購買了甲種商品20件,乙種商品x(x≥20)件.
(1)分別寫出優惠方案一購買費用y1(元)、優惠方案二購買費用y2(元)與所買乙種商品x(件)之間的函數關系式;
(2)若該公司共需要甲種商品20件,乙種商品40件.設按照方案一的優惠辦法購買了m件甲種商品,其余按方案二的優惠辦法購買.請你寫出總費用w與m之間的關系式;利用w與m之間的關系式說明怎樣購買最實惠.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com