
【題目】如圖,已知直線y=x+k和雙曲線y= ![]() (k為正整數(shù))交于A,B兩點(diǎn).
(k為正整數(shù))交于A,B兩點(diǎn).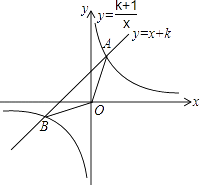
(1)當(dāng)k=1時,求A、B兩點(diǎn)的坐標(biāo);
(2)當(dāng)k=2時,求△AOB的面積;
(3)當(dāng)k=1時,△OAB的面積記為S1 , 當(dāng)k=2時,△OAB的面積記為S2 , …,依此類推,當(dāng)k=n時,△OAB的面積記為Sn , 若S1+S2+…+Sn= ![]() ,求n的值.
,求n的值.
【答案】
(1)解:當(dāng)k=1時,直線y=x+k和雙曲線y= ![]() 化為:y=x+1和y=
化為:y=x+1和y= ![]() ,
,
解 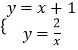 得
得 ![]() ,
, ![]() ,
,
∴A(1,2),B(﹣2,﹣1)
(2)解:當(dāng)k=2時,直線y=x+k和雙曲線y= ![]() 化為:y=x+2和y=
化為:y=x+2和y= ![]() ,
,
解 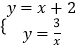 得
得 ![]() ,
, ![]() ,
,
∴A(1,3),B(﹣3,﹣1)
設(shè)直線AB的解析式為:y=mx+n,
∴ ![]()
∴ ![]() ,
,
∴直線AB的解析式為:y=x+2
∴直線AB與y軸的交點(diǎn)(0,2),
∴S△AOB= ![]() ×2×1+
×2×1+ ![]() ×2×3=4;
×2×3=4;
(3)解:當(dāng)k=1時,S1= ![]() ×1×(1+2)=
×1×(1+2)= ![]() ,
,
當(dāng)k=2時,S2= ![]() ×2×(1+3)=4,
×2×(1+3)=4,
…
當(dāng)k=n時,Sn= ![]() n(1+n+1)=
n(1+n+1)= ![]() n2+n,
n2+n,
∵S1+S2+…+Sn= ![]() ,
,
∴ ![]() ×(
×( ![]() …+n2)+(1+2+3+…n)=
…+n2)+(1+2+3+…n)= ![]() ,
,
整理得: ![]() ,
,
解得:n=6.
【解析】(1)兩圖像的交點(diǎn)就是求聯(lián)立的方程組的解;(2)斜三角形△AOB的面積可轉(zhuǎn)化為兩水平(或豎直)三角形(有一條邊為水平邊或豎直邊的三角形稱為水平或豎直三角形)的面積和或差;(3)利用n個數(shù)的平方和公式和等差數(shù)列的和公式可求出.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延長CA到O,使AO=AC,以O(shè)為圓心,OA長為半徑作⊙O交BA延長線于點(diǎn)D,連接CD.
(1)求證:CD是⊙O的切線;
(2)若AB=4,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)xOy中,正比例函數(shù)y=kx的圖象與反比例函數(shù)y= ![]() 的圖象都經(jīng)過點(diǎn)A(2,﹣2).
的圖象都經(jīng)過點(diǎn)A(2,﹣2).
(1)分別求這兩個函數(shù)的表達(dá)式;
(2)將直線OA向上平移3個單位長度后與y軸交于點(diǎn)B,與反比例函數(shù)圖象在第四象限內(nèi)的交點(diǎn)為C,連接AB,AC,求點(diǎn)C的坐標(biāo)及△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某汽車專賣店銷售![]() 、
、![]() 兩種型號的新能源汽車,上周售出1輛
兩種型號的新能源汽車,上周售出1輛![]() 型車和3輛
型車和3輛![]() 型車,銷售額為96萬元:本周售出2輛
型車,銷售額為96萬元:本周售出2輛![]() 型車和1輛
型車和1輛![]() 型車,銷售額為62萬元.
型車,銷售額為62萬元.
(1)求每輛車![]() 型車和
型車和![]() 型車的售價各多少萬元?
型車的售價各多少萬元?
(2)甲公司擬向該商店購買![]() 、
、![]() 兩種型號的新能源汽車共6輛,購車總費(fèi)用不超過140萬元,則至少購進(jìn)
兩種型號的新能源汽車共6輛,購車總費(fèi)用不超過140萬元,則至少購進(jìn)![]() 型車多少輛?
型車多少輛?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點(diǎn)O,過點(diǎn)O作EF∥BC交AB于E,交AC于F,過點(diǎn)O作OD⊥AC于D,下列四個結(jié)論:
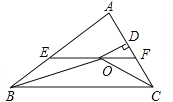
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③點(diǎn)O到△ABC各邊的距離相等;
④設(shè)OD=m,AE+AF=n,則![]() .
.
其中正確的結(jié)論是____.(填序號)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)A和動點(diǎn)P在直線l上,點(diǎn)P關(guān)于點(diǎn)A的對稱點(diǎn)為Q,以AQ為邊作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圓O.點(diǎn)C在點(diǎn)P右側(cè),PC=4,過點(diǎn)C作直線m⊥l,過點(diǎn)O作OD⊥m于點(diǎn)D,交AB右側(cè)的圓弧于點(diǎn)E.在射線CD上取點(diǎn)F,使DF= ![]() CD,以DE,DF為鄰邊作矩形DEGF.設(shè)AQ=3x.
CD,以DE,DF為鄰邊作矩形DEGF.設(shè)AQ=3x.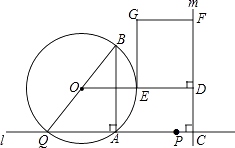
(1)用關(guān)于x的代數(shù)式表示BQ,DF.
(2)當(dāng)點(diǎn)P在點(diǎn)A右側(cè)時,若矩形DEGF的面積等于90,求AP的長.
(3)在點(diǎn)P的整個運(yùn)動過程中,
①當(dāng)AP為何值時,矩形DEGF是正方形?
②作直線BG交⊙O于點(diǎn)N,若BN的弦心距為1,求AP的長(直接寫出答案).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在長方形![]() 中,
中,![]() 為平面直角坐標(biāo)系的原點(diǎn),點(diǎn)
為平面直角坐標(biāo)系的原點(diǎn),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() 且
且![]() 滿足
滿足![]() ,點(diǎn)
,點(diǎn)![]() 在第一象限內(nèi),點(diǎn)
在第一象限內(nèi),點(diǎn)![]() 從原點(diǎn)出發(fā),以每秒
從原點(diǎn)出發(fā),以每秒![]() 個單位長度的速度沿著
個單位長度的速度沿著![]() 的線路移動.
的線路移動.
![]() 求點(diǎn)
求點(diǎn)![]() 的坐標(biāo)為 ;當(dāng)點(diǎn)
的坐標(biāo)為 ;當(dāng)點(diǎn)![]() 移動
移動![]() 秒時,點(diǎn)
秒時,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為
![]() 在移動過程中,當(dāng)點(diǎn)
在移動過程中,當(dāng)點(diǎn)![]() 移動
移動![]() 秒時,求
秒時,求![]() 的面積.
的面積.
![]() 在
在![]() 的條件下,坐標(biāo)軸上是否存在點(diǎn)
的條件下,坐標(biāo)軸上是否存在點(diǎn)![]() ,使
,使![]() 的面積與
的面積與![]() 的面積相等,若存在,求點(diǎn)
的面積相等,若存在,求點(diǎn)![]() 的坐標(biāo);若不存在,說明理由.
的坐標(biāo);若不存在,說明理由.
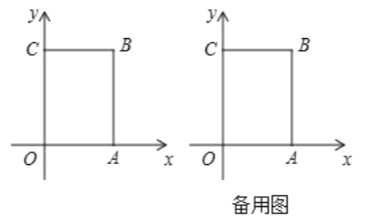
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC在直角坐標(biāo)系中.
(1)若把△ABC向上平移2個單位,再向左平移1個單位得到△A1B1C1,畫出△A1B1C1,并寫出點(diǎn)A1,B1,C1的坐標(biāo);
(2)求△ABC的面積.
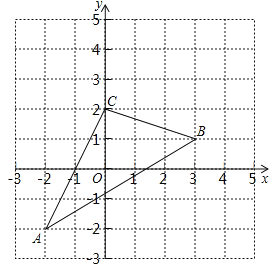
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點(diǎn)C為AB上一點(diǎn),作CD⊥AB交⊙O于D,連接AD,將△ACD沿AD翻折至△AC′D.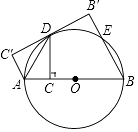
(1)請你判斷C′D與⊙O的位置關(guān)系,并說明理由;
(2)過點(diǎn)B作BB′⊥C′D′于B′,交⊙O于E,若CD= ![]() ,AC=3,求BE的長.
,AC=3,求BE的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com