
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(
兩點(![]() 在
在![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,過
,過![]() 點的直線
點的直線![]() :
:![]() 與
與![]() 軸交于點
軸交于點![]() ,與拋物線
,與拋物線![]() 的另一個交點為
的另一個交點為![]() ,己知
,己知![]() ,
,![]() ,
,![]() 點為拋物線
點為拋物線![]() 上一動點(不與
上一動點(不與![]() 、
、![]() 重合).
重合).
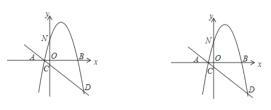
(1)直接寫出拋物線和直線![]() 的解析式;
的解析式;
(2)當點![]() 在直線
在直線![]() 上方的拋物線上時,連接
上方的拋物線上時,連接![]() 、
、![]() ,
,
①當![]() 的面積最大時,
的面積最大時,![]() 點的坐標是________;
點的坐標是________;
②當![]() 平分
平分![]() 時,求線段
時,求線段![]() 的長.
的長.
(3)設![]() 為直線
為直線![]() 上的點,探究是否存在點
上的點,探究是否存在點![]() ,使得以點
,使得以點![]() 、
、![]() ,
,![]() 、
、![]() 為頂點的四邊形為平行四邊形?若存在,直接寫出點
為頂點的四邊形為平行四邊形?若存在,直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②
,②![]() ;(3)存在,
;(3)存在,![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)將點A、D的坐標分別代入直線表達式、拋物線的表達式,即可求解;
(2)①先找出當![]() 的面積最大時,
的面積最大時,![]() 點的位置為與直線
點的位置為與直線![]() 平行且與拋物線相切的點,設直線解析式為
平行且與拋物線相切的點,設直線解析式為![]() ,即
,即![]() 有唯一解,求出
有唯一解,求出![]() 的值,再解方程求出x、y,即為P點的坐標;②過
的值,再解方程求出x、y,即為P點的坐標;②過![]() 作
作![]() 軸于
軸于![]() 點,由
點,由![]()
![]() 先求出
先求出![]() ,根據平分線定義得
,根據平分線定義得![]() ,設
,設![]() 點坐標為
點坐標為![]() ,依題意有
,依題意有![]() ,求出t的值,進而求得PA的長;
,求出t的值,進而求得PA的長;
(3)分NC是平行四邊形的一條邊、NC是平行四邊形的對角線,兩種情況分別求解即可.
解:(1)將點![]() 、
、![]() 的坐標代入直線表達式得:
的坐標代入直線表達式得:![]() ,解得:
,解得:![]() ,
,
故直線![]() 的表達式為:
的表達式為:![]() ,
,
將點![]() 、
、![]() 的坐標代入拋物線表達式,
的坐標代入拋物線表達式,
同理可得拋物線的表達式為:![]() ;
;
(2)①當![]() 的面積最大時,
的面積最大時,![]() 點到直線
點到直線![]() 的距離就最大,
的距離就最大,
所以![]() 點在與直線
點在與直線![]() 平行并且與拋物線相切的直線上,即
平行并且與拋物線相切的直線上,即![]() 點是這兩個圖像的唯一交點.
點是這兩個圖像的唯一交點.
設![]() 點坐標為
點坐標為![]() ,依題意有:
,依題意有:![]()
∴![]()
∵直線![]() 與拋物線相切,即只有一個交點
與拋物線相切,即只有一個交點
∴![]() ∴
∴![]()
∴![]()
∴![]() ∴
∴![]()
由此得![]() 點坐標為
點坐標為![]()
②過![]() 作
作![]() 軸于
軸于![]() 點,
點,
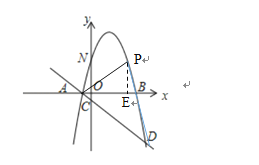
由直線![]() 的解析式
的解析式![]() ,可得
,可得![]()
![]()
∴![]()
∵![]() ∴
∴![]()
∴當![]() 平分
平分![]() 時,
時,![]() ,則
,則![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]()
設![]() 點坐標為
點坐標為![]() ,依題意有
,依題意有![]()
∴![]() ,
,![]() (舍去)
(舍去)
∴![]()
∴![]()
(3)![]() ,
,
①當![]() 是平行四邊形的一條邊時,
是平行四邊形的一條邊時,
設點![]() 坐標為
坐標為![]() 、則點
、則點![]() ,
,
由題意得:![]() ,即:
,即:![]() ,
,
解得:![]() 或0或4(舍去0),
或0或4(舍去0),
則:![]() 或
或![]() 或-5
或-5
則點![]() 坐標為
坐標為![]() 或
或![]() 或
或![]() ;
;
②當![]() 是平行四邊形的對角線時,
是平行四邊形的對角線時,
則![]() 的中點坐標為
的中點坐標為![]()
設點![]() 坐標為
坐標為![]() 、則點
、則點![]() ,
,
![]() 、
、![]() ,
,![]() 、
、![]() 為頂點的四邊形為平行四邊形,則
為頂點的四邊形為平行四邊形,則![]() 的中點即為
的中點即為![]() 中點,
中點,
即:![]() ,
,![]() ,
,
解得:![]() 或4(舍去0),d=﹣4,-d-1=3
或4(舍去0),d=﹣4,-d-1=3
故點![]() ;
;
故點M的坐標為:![]() 或
或![]() 或
或![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某單位在疫情期間用3000元購進A、B兩種口罩1100個,購買A種口罩與購買B種口罩的費用相同,且A種口罩的單價是B種口罩單價的1.2倍;
(1)求A,B兩種口罩的單價各是多少元?
(2)若計劃用不超過7000元的資金再次購進A、B兩種口罩共2600個,已知A、B兩種口罩的進價不變,求A種口罩最多能購進多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=﹣x+4與坐標軸交于A,B兩點,OC⊥AB于點C,P是線段OC上的一個動點,連接AP,將線段AP繞點A逆時針旋轉45°,得到線段AP',連接CP',則線段CP'的最小值為( )
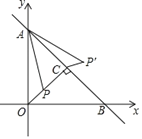
A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
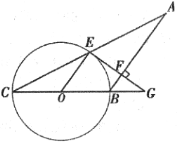
【題目】如圖,在△ABC中,AB=BC,以BC為直徑作⊙ O交AC于點E,過點E作AB的垂線交AB于點F,交CB的延長線于點G.
(1)求證:EG是⊙O的切線;
(2)若BG=OB,AC=6,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 繞
繞![]() 點旋轉
點旋轉![]() 得到
得到![]() ,
,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結論有______(只填寫序號).
.其中正確的結論有______(只填寫序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據完全平方公式可以作如下推導(a、b都為非負數)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其實,這個不等關系可以推廣,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非負數)
(以上an都是非負數)
我們把這種關系稱為:算術—幾何均值不等式
例如:x為非負數時,![]() ,則
,則![]() 有最小值.
有最小值.
再如:x為非負數時,x+x+![]() .
.
我們來研究函數:![]()

(1)這個函數的自變量x的取值范圍是 ;
(2)完成表格并在坐標系中畫出這個函數的大致圖象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根據算術—幾何均值不等式,該函數在第一象限有最 值,是 ;
(4)某同學在研究這個函數時提出這樣一個結論:當x>a時,y隨x增大而增大,則a的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,共享單車逐漸成為高校學生喜愛的“綠色出行”方式之一,許多高校均投放了使用手機支付就可隨取隨用的共享單車.某高校為了解本校學生出行使用共享單車的情況,隨機調查了某天部分出行學生使用共享單車的情況,并整理成如下統計表.
使用次數(次) | 0 | 1 | 2 | 3 | 4 | 5 |
人數(人) | 11 | 15 | 23 | 28 | 20 | 3 |
(1)這天部分出行學生使用共享單車次數的眾數是_________(次).
(2)求這天部分出行學生平均每人使用共享單車的次數.
(3)若該校某天有1500名學生出行,請你估計這天使用共享單車次數在3次以上(含3次)的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校七年級共有500名學生,為了解該年級學生的課外閱讀情況,將從中隨機抽取的40名學生一個學期的閱讀量(閱讀書籍的本數)作為樣本,根據數據繪制了如下的表格和統計圖:
等級 | 閱讀量( | 頻數 | 頻率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |

根據上面提供的信息,回答下列問題:
(1)統計表中的![]() ,
,![]() ;并補全條形統計圖;
;并補全條形統計圖;
(2)根據抽樣調查結果,請估計該校七年級學生一學期的閱讀量為“![]() 等”的有多少人?
等”的有多少人?
(3)樣本中閱讀量為“![]() 等”的4名學生中有2名男生和2名女生,現從中隨機挑選2名同學參加區里舉行的“語文學科素養展示”活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
等”的4名學生中有2名男生和2名女生,現從中隨機挑選2名同學參加區里舉行的“語文學科素養展示”活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com