
【題目】已知拋物線![]() 的頂點
的頂點![]() 在
在![]() 軸上.
軸上.
(1)若點![]() 是拋物線最低點,且落在
是拋物線最低點,且落在![]() 軸正半軸上,直接寫出
軸正半軸上,直接寫出![]() 的取值范圍;
的取值范圍;
(2)![]() ,
,![]() 是拋物線上兩點,若
是拋物線上兩點,若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() ,且當
,且當![]() 的絕對值為4時,
的絕對值為4時,![]() 為等腰直角三角形(其中
為等腰直角三角形(其中![]() ).
).
①求拋物線的解析式;
②設![]() 中點為
中點為![]() ,若
,若![]() ,求點
,求點![]() 縱坐標的最小值.
縱坐標的最小值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②當
;②當![]() 時,
時,![]() 最小值是2.
最小值是2.
【解析】
(1)由頂點![]() 是拋物線最低點,可判斷拋物線開口向上,可判定a的符號;根據拋物線的解析式確定頂點坐標,根據頂點A落在
是拋物線最低點,可判斷拋物線開口向上,可判定a的符號;根據拋物線的解析式確定頂點坐標,根據頂點A落在![]() 軸正半軸上,可判定h、k的取值范圍;
軸正半軸上,可判定h、k的取值范圍;
(2)①由已知可得當x<0時,y隨x的增大而減小,當x>0時,y隨x的增大而增大,所以對稱軸為![]() 軸,即可確定拋物線為y=ax2,再由△APQ為等腰直角三角形和y1的絕對值為4,得到a=
軸,即可確定拋物線為y=ax2,再由△APQ為等腰直角三角形和y1的絕對值為4,得到a=![]() ;
;
②設N點坐標為(x,y),PQ2=8y+4y2-![]() (x1x2+4)2+4≥36,所以4(y+1)2≥36+
(x1x2+4)2+4≥36,所以4(y+1)2≥36+![]() (x1x2+4)2,當x1x2=-4時,y有最小值,y+1≥3,y≥2, 即N點縱坐標最小值為2.
(x1x2+4)2,當x1x2=-4時,y有最小值,y+1≥3,y≥2, 即N點縱坐標最小值為2.
(1)∵拋物線有最低點,
∴a>0,
∵拋物線的頂點坐標為(h,k)在x軸正半軸上,
∴h>0,k=0;
(2)①∵當![]() 時,
時,![]() ;則
;則![]() ,
,
∴當x<0時,y隨x的增大而減小,
當![]() 時,
時,![]() ;則
;則![]()
∴當x>0時,y隨x的增大而增大,
∴拋物線的對稱軸是![]() 軸,且開口向上
軸,且開口向上
又頂點在![]() 軸上,所以頂點是原點
軸上,所以頂點是原點![]()
∴拋物線的解析式為![]() ,且
,且![]()
當![]() 是等腰直角三角形,
是等腰直角三角形,![]() 時,
時,![]() ,
,
又![]() 為頂點,所以點
為頂點,所以點![]() 關于拋物線對稱軸
關于拋物線對稱軸![]() 軸對稱.
軸對稱.
![]() ,
,![]()
∴![]()
設![]() 交
交![]() 軸于點
軸于點![]() ,則
,則![]() ,
,
∴點![]() 中一個坐標為
中一個坐標為![]() ,另一個為
,另一個為![]()
把![]() 代入
代入![]() ,解得
,解得![]()
∴拋物線的解析式為![]()
②PQ2=(x1-x2)2+(y1-y2)2≥36,
∵y1=![]() x12,y2=
x12,y2=![]() x22,
x22,
∴PQ2=(x1-x2)2+(y1-y2)2
=(x1-x2)2+(![]() x12-
x12-![]() x22)2
x22)2
=(x1-x2)2+![]() (x12+x22)2-
(x12+x22)2-![]() x12x22
x12x22
=x12+x22-2x1x2+![]() (x12+x22)2-
(x12+x22)2-![]() x12x22
x12x22
=4(y1+y2)+(y1+y2)2-![]() (x12x22+8x1x2)
(x12x22+8x1x2)
=4(y1+y2)+(y1+y2)2-![]() (x12x22+8x1x2+16-16)
(x12x22+8x1x2+16-16)
=4(y1+y2)+(y1+y2)2-![]() (x1x2+4)2+4
(x1x2+4)2+4
∵設N點坐標為(x,y),N是PQ的中點,
∴![]() >0
>0
∴2x=x1+x2,2y=y1+y2,
∴PQ2=8y+4y2-![]() (x1x2+4)2+4≥36,
(x1x2+4)2+4≥36,
∴4(y+1)2≥36+![]() (x1x2+4)2,
(x1x2+4)2,
∵y+1>0
當x1x2=-4時,y有最小值,
∴y+1≥3,
∴y≥2,
∴點N縱坐標的最小值為2


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】 愛好數學的甲、乙兩個同學做了一個數字游戲:拿出三張正面寫有數字-1,0,1且背面完全相同的卡片,將這三張卡片背面朝上洗勻后,甲先隨機抽取一張,將所得數字作為p的值,然后將卡片放回并洗勻,乙再從這三張卡片中隨機抽取一張,將所得數字作為q值,兩次結果記為(p,q).
(1)請你幫他們用樹狀圖或列表法表示(p,q)所有可能出現的結果;
(2)求滿足關于x的方程x2+px+q=0有實數根的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:拋物線y=x2+bx+c與x軸交于A(﹣1,0),B(3,0)兩點,與y軸交于點C,點D為頂點,連接BD,CD,拋物線的對稱軸與x軸交與點E.
(1)求拋物線解析式及點D的坐標;
(2)G是拋物線上B,D之間的一點,且S四邊形CDGB=4S△DGB,求出G點坐標;
(3)在拋物線上B,D之間是否存在一點M,過點M作MN⊥CD,交直線CD于點N,使以C,M,N為頂點的三角形與△BDE相似?若存在,求出滿足條件的點M的坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2+(a+3)x+3(a≠0)與x軸交于點A(4,0),與y軸交于點B,在x軸上有一動點E(m,0)(0<m<4),過點E作x軸的垂線交直線AB于點N,交拋物線于點P,過點P作PM⊥AB于點M.
(1)求a的值和直線AB的函數表達式;
(2)設△PMN的周長為C1,△AEN的周長為C2,若![]() ,求m的值;
,求m的值;
(3)如圖2,在(2)條件下,將線段OE繞點O逆時針旋轉得到OE′,旋轉角為α(0°<α<90°),連接AE′、BE′,求AE′+![]() BE′的最小值.
BE′的最小值.
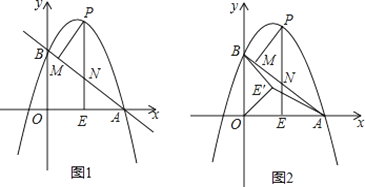
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象相交于 A,B 兩點,與 x 軸相交于點 C.已知 tan∠BOC=
的圖象相交于 A,B 兩點,與 x 軸相交于點 C.已知 tan∠BOC=![]() ,點 B 的坐標為(m,n).
,點 B 的坐標為(m,n).
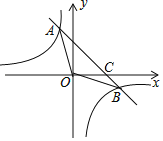
(1)求反比例函數的解析式;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ECFD各頂點在Rt△ABC的邊上,觀察圖形,并回答下列問題:
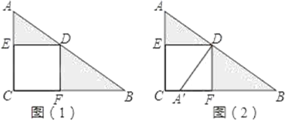
(1)請你說明由圖(1)變換到圖(2)的過程;
(2)若AD=3,△AED與△BDF的面積和為9,求線段BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在△ABC中,AB>AC,點D,E分別在邊AB,AC上,且DE∥BC,若AD=2,AE=![]() ,則
,則![]() 的值是 ;
的值是 ;
(2)如圖2,在(1)的條件下,將△ADE繞點A逆時針方向旋轉一定的角度,連接CE和BD,![]() 的值變化嗎?若變化,請說明理由;若不變化,請求出不變的值;
的值變化嗎?若變化,請說明理由;若不變化,請求出不變的值;
(3)如圖3,在四邊形ABCD中,AC⊥BC于點C,∠BAC=∠ADC=θ,且tanθ=![]() ,當CD=6,AD=3時,請直接寫出線段BD的長度.
,當CD=6,AD=3時,請直接寫出線段BD的長度.
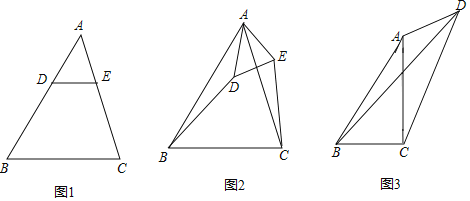
查看答案和解析>>
科目:初中數學 來源: 題型:
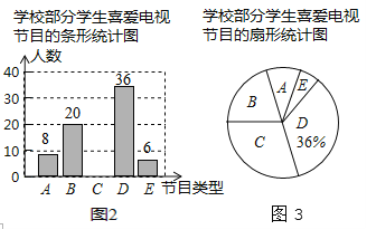
【題目】為了了解本校學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況,課題小組隨機選取該校部分學生進行了問卷調査(問卷調査表如圖1所示),并根據調查結果繪制了圖2、圖3兩幅統計圖(均不完整),請根據統計圖解答下列問題.
(1)本次接受問卷調查的學生有________名.
(2)補全條形統計圖.
(3)扇形統計圖中B類節目對應扇形的圓心角的度數為________.
(4)該校共有2000名學生,根據調查結果估計該校最喜愛新聞節目的學生人數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com