
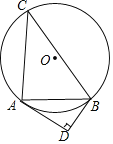
【題目】如圖,已知⊙O的半徑為5,△ABC是⊙O的內(nèi)接三角形,AB=8,.過(guò)點(diǎn)B作⊙O的切線BD,過(guò)點(diǎn)A作AD⊥BD,垂足為D.
(1)求證:∠BAD+∠C=90°
(2)求線段AD的長(zhǎng).
【答案】(1)證明見(jiàn)解析;(2)![]() .
.
【解析】
(1)由弦切角等于同弧所對(duì)的圓周角得:∠C=∠ABD,再根據(jù)直角三角形兩銳角互余得出結(jié)論;
(2)作弦心距,由勾股定理得:OE=3,再證明△OEB∽△BDA,列比例式可以求AD的長(zhǎng).
:(1)∵BD為⊙O的切線,
∴∠C=∠ABD,
∵AD⊥BD,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∴∠C+∠BAD=90°,
(2)連接OB,過(guò)O作OE⊥AB于E,
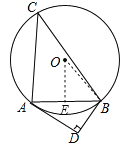
∴AE=BE=![]() AB=4,
AB=4,
由勾股定理得:OE=![]() =
=![]() =3,
=3,
∵BD為⊙O的切線,
∴OB⊥BD,
∴∠OBD=90°,
∵∠ADB=90°,
∴AD∥OB,
∴∠DAB=∠ABO,
∵∠D=∠OEB=90°,
∴△OEB∽△BDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ;
;
則線段AD的長(zhǎng)為![]() .
.


 星級(jí)口算天天練系列答案
星級(jí)口算天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】2019年5月9日,美國(guó)政府宣布自2019年5月10日起,對(duì)中國(guó)進(jìn)口的![]() 億美元清單商品加征的關(guān)稅稅率由
億美元清單商品加征的關(guān)稅稅率由![]() 提高到
提高到![]() .為了解我校師生對(duì)此事的關(guān)注度,學(xué)生張明采取隨機(jī)抽樣的方法進(jìn)行問(wèn)卷調(diào)查,繪制了如下兩幅不完整的統(tǒng)計(jì)圖,請(qǐng)結(jié)合圖中所給的信息解答下列問(wèn)題: 我校師生對(duì)“加征關(guān)稅稅率”了解情況條形統(tǒng)計(jì)圍我校師生對(duì)“加征關(guān)稅稅率”了解情況扇形統(tǒng)計(jì)圍
.為了解我校師生對(duì)此事的關(guān)注度,學(xué)生張明采取隨機(jī)抽樣的方法進(jìn)行問(wèn)卷調(diào)查,繪制了如下兩幅不完整的統(tǒng)計(jì)圖,請(qǐng)結(jié)合圖中所給的信息解答下列問(wèn)題: 我校師生對(duì)“加征關(guān)稅稅率”了解情況條形統(tǒng)計(jì)圍我校師生對(duì)“加征關(guān)稅稅率”了解情況扇形統(tǒng)計(jì)圍
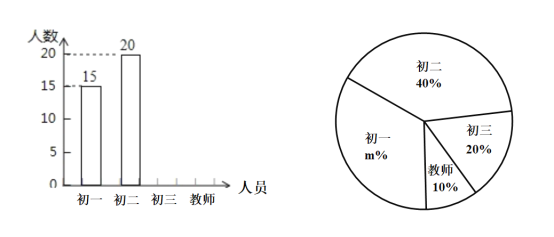
![]() 本次調(diào)查的人數(shù)有 人, 在扇形統(tǒng)計(jì)圖中,
本次調(diào)查的人數(shù)有 人, 在扇形統(tǒng)計(jì)圖中,![]() 的值是 ;請(qǐng)將條形統(tǒng)計(jì)圖補(bǔ)充完整.
的值是 ;請(qǐng)將條形統(tǒng)計(jì)圖補(bǔ)充完整.
![]() 在被調(diào)查的教師中,有
在被調(diào)查的教師中,有![]() 男
男![]() 女共
女共![]() 名教師愿意接受深入調(diào)查,現(xiàn)要從這
名教師愿意接受深入調(diào)查,現(xiàn)要從這![]() 名教師中隨機(jī)抽取
名教師中隨機(jī)抽取![]() 名教
名教
師進(jìn)行深入調(diào)查,請(qǐng)畫(huà)樹(shù)狀圖或者列表求出所抽取的![]() 名教師恰好是
名教師恰好是![]() 名男教師和
名男教師和![]() 名女教師的概率.
名女教師的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
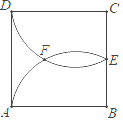
【題目】如圖,正方形ABCD的邊長(zhǎng)為2a,E為BC邊的中點(diǎn),![]() 的圓心分別在邊AB、CD上,這兩段圓弧在正方形內(nèi)交于點(diǎn)F,則E、F間的距離為 .
的圓心分別在邊AB、CD上,這兩段圓弧在正方形內(nèi)交于點(diǎn)F,則E、F間的距離為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】房山某中學(xué)改革學(xué)生的學(xué)習(xí)模式,變“老師要學(xué)生學(xué)習(xí)”為“學(xué)生自主學(xué)習(xí)”,培養(yǎng)了學(xué)生自主學(xué)習(xí)的能力.小華與小明同學(xué)就“最喜歡哪種學(xué)習(xí)方式”隨機(jī)調(diào)查了他們周?chē)囊恍┩瑢W(xué),根據(jù)收集到的數(shù)據(jù)繪制了以下的兩個(gè)統(tǒng)計(jì)圖.請(qǐng)根據(jù)下面兩個(gè)不完整的統(tǒng)計(jì)圖回答以下問(wèn)題:

(1)這次抽樣調(diào)查中,共調(diào)查了 名學(xué)生;
(2)補(bǔ)全兩幅統(tǒng)計(jì)圖;
(3)根據(jù)抽樣調(diào)查的結(jié)果,估算該校1000名學(xué)生中大約有多少人選擇“小組合作學(xué)習(xí)”?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
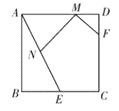
【題目】如圖,在正方形ABCD中,AB=4,E是BC邊的中點(diǎn), F是CD邊上的一點(diǎn), 且DF=1.若M、N分別是線段AD、AE上的動(dòng)點(diǎn),則MN+MF的最小值為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
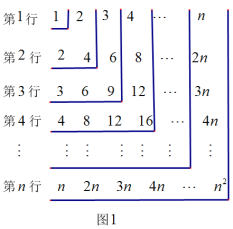
【題目】如圖1,觀察數(shù)表,如何計(jì)算數(shù)表中所有數(shù)的和?
方法1:如圖1,先求每行數(shù)的和:
第1行 ![]()
第2行 ![]()
第n行 ![]()
故表中所有數(shù)的和:
![]() ;
;

方法2:如圖2.依次以第1行每個(gè)數(shù)為起點(diǎn),按順時(shí)針?lè)较蛴?jì)算各數(shù)的和:
第1組 ![]()
第2組 ![]()
第3組 ![]()
…
第![]() 組
組 ![]() ,
,
用這![]() 組數(shù)計(jì)算的結(jié)果,表示數(shù)表中所有數(shù)的和為: ,
組數(shù)計(jì)算的結(jié)果,表示數(shù)表中所有數(shù)的和為: ,
綜合上面兩種方法所得的結(jié)果可得等式: ;
利用上面得到的規(guī)律計(jì)算:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校積極開(kāi)展“陽(yáng)光體育”活動(dòng),并開(kāi)設(shè)了跳繩、足球、籃球、跑步四種運(yùn)動(dòng)項(xiàng)目,為了解學(xué)生最喜愛(ài)哪一種項(xiàng)目,隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查,并繪制了如下的條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖(部分信息未給出).
(1)求本次被調(diào)查的學(xué)生人數(shù);
(2)補(bǔ)全條形統(tǒng)計(jì)圖;
(3)該校共有3000名學(xué)生,請(qǐng)估計(jì)全校最喜愛(ài)籃球的人數(shù)比最喜愛(ài)足球的人數(shù)多多少?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知一個(gè)三角形紙片![]() ,其中
,其中![]() ,
,![]() 分別是
分別是![]() 邊上的點(diǎn),連接
邊上的點(diǎn),連接![]() .
.
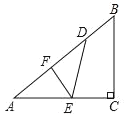
(1)如圖,若將紙片![]() 的一角沿
的一角沿![]() 折疊,折疊后點(diǎn)
折疊,折疊后點(diǎn)![]() 落在
落在![]() 邊上的點(diǎn)
邊上的點(diǎn)![]() 處,且使S四邊形ECBF
處,且使S四邊形ECBF![]() ,求
,求![]() 的長(zhǎng);
的長(zhǎng);
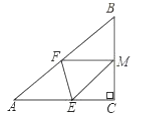
(2)如圖,若將紙片![]() 的一角沿
的一角沿![]() 折疊,折疊后點(diǎn)
折疊,折疊后點(diǎn)![]() 落在
落在![]() 邊上的點(diǎn)
邊上的點(diǎn)![]() 處,且使
處,且使![]() .試判斷四邊形
.試判斷四邊形![]() 的形狀,并證明你的結(jié)論.
的形狀,并證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
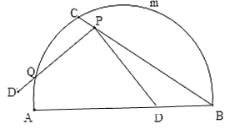
【題目】如圖,C是![]() 的一定點(diǎn),D是弦AB上的一定點(diǎn),P是弦CB上的一動(dòng)點(diǎn).連接DP,將線段PD繞點(diǎn)P順時(shí)針旋轉(zhuǎn)
的一定點(diǎn),D是弦AB上的一定點(diǎn),P是弦CB上的一動(dòng)點(diǎn).連接DP,將線段PD繞點(diǎn)P順時(shí)針旋轉(zhuǎn)![]() 得到線段
得到線段![]() .射線
.射線![]() 與
與![]() 交于點(diǎn)Q.已知
交于點(diǎn)Q.已知![]() ,設(shè)P,C兩點(diǎn)間的距離為xcm,P,D兩點(diǎn)間的距離
,設(shè)P,C兩點(diǎn)間的距離為xcm,P,D兩點(diǎn)間的距離![]() ,P,Q兩點(diǎn)的距離為
,P,Q兩點(diǎn)的距離為![]() .
.
小石根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),分別對(duì)函數(shù)![]() ,
,![]() ,隨自變量x的變化而變化的規(guī)律進(jìn)行了探究,下面是小石的探究過(guò)程,請(qǐng)補(bǔ)充完整:
,隨自變量x的變化而變化的規(guī)律進(jìn)行了探究,下面是小石的探究過(guò)程,請(qǐng)補(bǔ)充完整:
(1)按照下表中自變量x的值進(jìn)行取點(diǎn)、畫(huà)圖、測(cè)量,分別得到了![]() ,
,![]() ,與x的幾組對(duì)應(yīng)值:
,與x的幾組對(duì)應(yīng)值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐標(biāo)系xOy中,描出補(bǔ)全后的表中各組數(shù)據(jù)所對(duì)應(yīng)的點(diǎn)![]() ,
,![]() ,并畫(huà)出函數(shù)
,并畫(huà)出函數(shù)![]() ,
,![]() 的圖象;
的圖象;
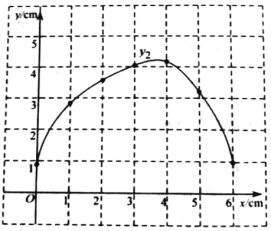
(3)結(jié)合函數(shù)圖象,解決問(wèn)題:連接DQ,當(dāng)△DPQ為等腰三角形時(shí),PC的長(zhǎng)度約為_____cm.(結(jié)果保留一位小數(shù))
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com