
【題目】如圖,E,F分別是矩形ABCD的邊AD,AB上的點,若EF=EC,且EF⊥EC.
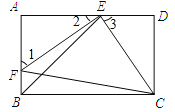
(1)求證:AE=DC;
(2)已知DC=![]() ,求BE的長.
,求BE的長.
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,矩形ABCD,AB=6cm,AD=8cm,點O從點B出發(fā),以1cm/s的速度向點C運動,設O點運動時間為t(單位:s)(0<t<4),以點O為圓心,OB為半徑作半圓⊙O交BC 于點M,過點A作⊙O的切線交BC于點N,切點為P.

(1)如圖2,當點N與點C重合時,求t;
(2)如圖3,連接AO,作OQ![]() AO交AN于點Q,連接QM,求證:QM是⊙O的切線;
AO交AN于點Q,連接QM,求證:QM是⊙O的切線;
(3)如圖4,連接CP,在點O整個運動過程中,求CP的最小值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
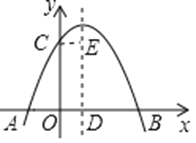
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與y軸交于點C,與x軸交于A,B兩點,其中點B的坐標為B(4,0),拋物線的對稱軸交x軸于點D,CE∥AB,并與拋物線的對稱軸交于點E.現(xiàn)有下列結(jié)論:①a>0;②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正確結(jié)論的序號是 _____________________ .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
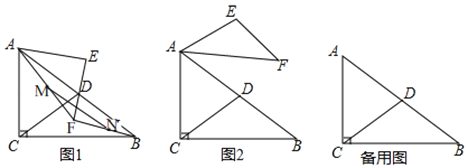
【題目】在Rt△ABC中,∠ACB=90°,AC=BC,CD為AB邊上的中線.在Rt△AEF中,∠AEF=90°,AE=EF,AF<AC.連接BF,M,N分別為線段AF,BF的中點,連接MN.
(1)如圖1,點F在△ABC內(nèi),求證:CD=MN;
(2)如圖2,點F在△ABC外,依題意補全圖2,連接CN,EN,判斷CN與EN的數(shù)量關(guān)系與位置關(guān)系,并加以證明;
(3)將圖1中的△AEF繞點A旋轉(zhuǎn),若AC=a,AF=b(b<a),直接寫出EN的最大值與最小值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E,AM是△ACD的外角∠DAF的平分線.

(1)求證:AM是⊙O的切線;
(2)若∠D = 60°,AD = 2,射線CO與AM交于N點,請寫出求ON長的思路.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
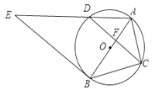
【題目】如圖,⊙O是△ABC的外接圓,AB經(jīng)過點O,CD是弦,且CD⊥AB于點F,連接AD,過點B的直線與線段AD的延長線交于點E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周長;
, AF=3,求⊙O的周長;
(2)求證:直線BE是⊙O的切線.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(換元思想)閱讀材料:
材料1 若一元二次方程![]() 的兩根為
的兩根為![]() 、
、![]() ,則
,則![]() ,
,![]() .
.
材料2 已知實數(shù)![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:由題知![]() 、
、![]() 是方程
是方程![]() 的兩個不相等的實數(shù)根,根據(jù)材料1,得
的兩個不相等的實數(shù)根,根據(jù)材料1,得![]() ,
,![]() .
.
∴![]() .
.
根據(jù)上述材料解決下面的問題:
(1)一元二次方程![]() 的兩根為
的兩根為![]() ,
,![]() ,則
,則![]() ,
,![]() ___________;
___________;
(2)已知實數(shù)![]() ,
,![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)已知實數(shù)![]() ,
,![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,且點C為⊙O上的一點,∠BAC=30°,M是OA上一點,過M作AB的垂線交AC于點N,交BC的延長線于點E,直線CF交EN于點F,且∠ECF=∠E.
(1)證明:CF是⊙O的切線;
(2)設⊙O的半徑為1,且AC=CE,求MO的長.
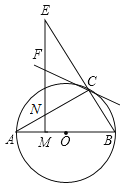
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com