名校課堂系列答案科目：初中數學 來源：學習周報 數學 北師大九年級版 2009－2010學年 第1期 總第157期 北師大版 題型：013
適合下列條件的△ABC(BC＝a，AB＝c，AC＝b)中，直角三角形的個數為
①a＝
，b＝
，c＝
；
②a＝b，∠A＝45°；
③∠A＝32°，∠B＝58°；
④a＝7，b＝24，c＝25．
1個
2個
3個
4個
查看答案和解析>>
科目：初中數學 來源：三點一測叢書 九年級數學 上 （江蘇版課標本） 江蘇版課標本 題型：044
實踐與探索課上，老師布置了這樣一道題：
有100米長的籬笆材料，想圍成一矩形露天倉庫，要求面積不小于600平方米，在場地的北面有一堵長50米的舊墻．有人用這個籬笆圍一個長40米，寬10米的矩形倉庫，但面積只有400平方米，不合要求．現在請你設計矩形倉庫的長和寬，使它符合要求．
經過同學們一天的實踐與思考，老師收到了如下幾種設計方案：
(1)如果設矩形的寬為x米，則用于長的籬笆為
＝(50－x)米，這時面積S＝x(50－x)．
當S＝600時，由x(50－x)＝600，得x2－50x＋600＝0，解得x1＝20，x2＝30．
檢驗后知x＝20符合要求．
(2)根據在周長相等的條件下，正方形面積大于矩形面積，所以設計成正方形倉庫，它的邊長為x米，則4x＝100，x＝25．這時面積達到625米，當然符合要求．
(3)如果利用場地北面的那堵舊墻，取矩形的長與舊墻平行，設與墻垂直的矩形一邊長為x米，則另一邊為100－2x，如圖．
因為舊墻長50米，所以100－2x≤50．即x≥25米．若S＝600平方米，則由x(100－2x)＝600，即x2－50x＋300＝0，解得x1＝25＋
，x2＝25－．根據x≥25，舍去x2＝25－．
所以，利用舊墻，取矩形垂直于舊墻一邊長為25＋米(約43米)，另一邊長約14米，符合要求．
(4)如果充分利用北面舊墻，即矩形一邊是50米舊墻時，用100米籬笆圍成矩形倉庫，則矩形另一邊長為25米，這時矩形面積為S＝50×25＝1250(平方米)．即面積可達1250平方米，符合設計要求．
還可以有其他一些符合要求的設計方案．請你試試看．
查看答案和解析>>
科目：初中數學 來源： 題型：013
BC的延長線交DE于F, ∠B＝∠D＝25°,∠ACB＝∠AED＝105°, ∠DAC＝10°, 則∠DFB的度數為
[ ]
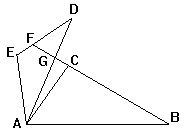
A.40° B.50° C.55° D.60°
查看答案和解析>>
科目：初中數學 來源： 題型：013
如圖所示, BD和CE是△ABC的高, BD和CE交于M,
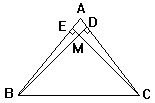
①圖中有____個直角三角形;
②設∠DBC＝25°, ∠ECB＝40°, 則 ∠EMD ＝_______度,
③∠DMC＝____度, ④∠A ＝______度.
① A.6 B.5 C.4 D.3
② A.100° B.115° C.125° D.250°
③ A.60° B.55° C.65° D.70°
④ A.65° B.50° C.45° D.40°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
＝±25
