
【題目】某商場為了吸引顧客,設立一個可自由轉動的轉盤,(如圖,3個數字所在的扇形面積相等)并規定,顧客每購滿100元商品,可轉動兩次轉盤,轉盤停止后,看指針指向的數.(如果指針指向分界線,則重新轉動轉盤,直到指針指向數為止)獲獎方法是:①指針兩次都指向3,顧客可獲得90元購物券,②指針只有一次指向3,顧客可得36元購物券,③指針兩次都不指向3,顧客只能獲得18元購物券;若顧客不愿轉動轉盤,則可直接獲得30元購物券
(1)試用樹狀圖或列表法給出兩次轉動轉盤指針所有可能指向的結果;
(2)請分別求顧客獲得90元,36元,18元購物券的概率;
(3)你認為轉動轉盤和直接獲得購物券哪種方式更合算?試說明理由.

【答案】(1)詳見解析;(2)![]() ;(3)轉動轉盤合算.
;(3)轉動轉盤合算.
【解析】
(1)用列表法列舉出所有情況,看所求的情況與總情況的比值即可得答案;
(2)由(1)的圖表,根據題意分析可得顧客獲得90元、36元、18元購物券的情況數目,根據概率公式可得答案;
(3)算出每轉動兩次轉盤所獲得購物券金額的平均數,與直接獲得購物券比較可得答案.
解:(1)如下表:
1 | 2 | 3 | |
1 | (1,1) | (2,1) | (3,1) |
2 | (1,2) | (2,2) | (3,2) |
3 | (1,3) | (2,3) | (3,3) |
(2)P(獲得90元)=![]() ,P(獲得36元)=
,P(獲得36元)=![]() ,P(獲得18元)=
,P(獲得18元)=![]() ;
;
(3)轉動轉盤合算,
每轉動兩次轉盤所獲得購物券金額的平均數為:![]() ,
,
所以轉動轉盤合算.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在二次函數y=ax2+bx+c(a≠0)的圖象中,小明同學觀察得出了下面幾條信息:①b2﹣4ac>0;②abc<0;③![]() ;④b2=4a(c﹣1);⑤關于x的一元二次方程ax2+bx+c=3無實數根,共中信息錯誤的個數為( )
;④b2=4a(c﹣1);⑤關于x的一元二次方程ax2+bx+c=3無實數根,共中信息錯誤的個數為( )
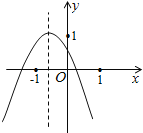
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
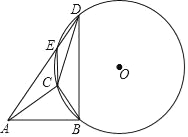
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=5,過點B作BD⊥AB,點C,D都在AB上方,AD交△BCD的外接圓⊙O于點E.
(1)求證:∠CAB=∠AEC.
(2)若BC=3.
①EC∥BD,求AE的長.
②若△BDC為直角三角形,求所有滿足條件的BD的長.
(3)若BC=EC=![]()
![]() ,則
,則![]() = .(直接寫出結果即可)
= .(直接寫出結果即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
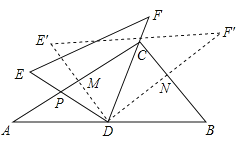
【題目】將一副三角尺(在RtΔABC中,∠ACB=90°,∠B=60°;在RtΔEDF中,∠EDF=90°,∠E=45°)如圖擺放,點D為AB的中點,DE交AC于點P,DF經過點C.將RtΔEDF繞點D順時針方向旋轉角α(0°<α<60°), DE交AC于點M,DF交BC于點N,則![]() 的值為( )
的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出
(1)如圖①,在△ABC中,∠A=120°,AB=AC=5,則△ABC的外接圓半徑R的值為 .
問題探究
(2)如圖②,⊙O的半徑為13,弦AB=24,M是AB的中點,P是⊙O上一動點,求PM的最大值.
問題解決
(3)如圖③所示,AB、AC、BC是某新區的三條規劃路其中,AB=6km,AC=3km,∠BAC=60°,BC所對的圓心角為60°.新區管委會想在BC路邊建物資總站點P,在AB、AC路邊分別建物資分站點E、F.也就是,分別在![]() 、線段AB和AC上選取點P、E、F.由于總站工作人員每天要將物資在各物資站點間按P→E→F→P的路徑進行運輸,因此,要在各物資站點之間規劃道路PE、EF和FP.為了快捷環保和節約成本要使得線段PE、EF、FP之和最短,試求PE+EF+FP的最小值(各物資站點與所在道路之間的距離、路寬均忽略不計).
、線段AB和AC上選取點P、E、F.由于總站工作人員每天要將物資在各物資站點間按P→E→F→P的路徑進行運輸,因此,要在各物資站點之間規劃道路PE、EF和FP.為了快捷環保和節約成本要使得線段PE、EF、FP之和最短,試求PE+EF+FP的最小值(各物資站點與所在道路之間的距離、路寬均忽略不計).



圖① 圖② 圖③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線![]() 與x軸交于點A,與y軸交于點C,拋物線
與x軸交于點A,與y軸交于點C,拋物線![]() 經過A、C兩點,與x軸的另一交點為點B.
經過A、C兩點,與x軸的另一交點為點B.
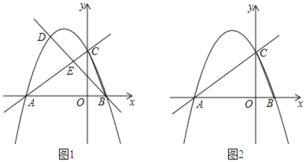
(1)求拋物線的函數表達式;(2)點D為直線AC上方拋物線上一動點,
①連接BC、CD、BD,設BD交直線AC于點E,△CDE的面積為S1,△BCE的面積為S2.求:![]() 的最大值;
的最大值;
②如圖2,是否存在點D,使得∠DCA=2∠BAC?若存在,直接寫出點D的坐標,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從共享單車,共享汽車等共享出行到共享雨傘等共享物品,各式各樣的共享經濟模式在各個領域迅速的普及,根據國家信息中心發布的中國分享經濟發展報告2017顯示,參與共享經濟活動超6 億人,比上一年增加約1億人.
(1)為獲得北京市市民參與共享經濟活動信息,下列調查方式中比較合理的是 ;
A.對某學校的全體同學進行問卷調查
B.對某小區的住戶進行問卷調查
C.在全市里的不同區縣,選取部分市民進行問卷調查
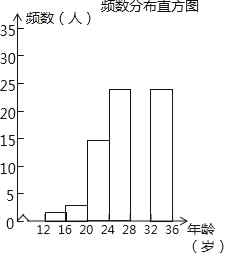
(2)調查小組隨機調查了延慶區市民騎共享單車情況,某社區年齡在12~36歲的人有1000人,從中隨機抽取了100人,統計了他們騎共享單車的人數,并繪制了如下不完整的統計圖表.如圖所示.騎共享單車的人數統計表
年齡段(歲) | 頻數 | 頻率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
根據以上信息解答下列問題:
①統計表中的a= ;b= ;
②補全頻數分布直方圖;
③試估計這個社區年齡在20歲到32歲(含20歲,不含32歲)騎共享單車的人有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,反比例函數y=![]() 的圖象與一次函數y=k(x-2)的圖象交點為A(3,2),B(x,y).
的圖象與一次函數y=k(x-2)的圖象交點為A(3,2),B(x,y).
(1)求反比例函數與一次函數的解析式及B點坐標;
(2)若C是y軸上的點,且滿足△ABC的面積為10,求C點坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
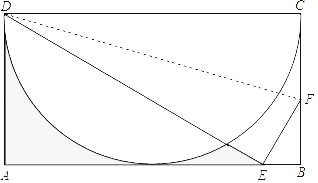
【題目】如圖所示,ABCD為矩形,以CD為直徑作半圓,矩形的另外三邊分別與半圓相切,沿著折痕DF折疊該矩形,使得點C的對應點E落在AB邊上,若AD=2,則圖中陰影部分的面積為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com