
【題目】已知:如圖①,在□ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向勻速平移得到△PNM,
速度為1cm/s;同時(shí),點(diǎn)Q從點(diǎn)C出發(fā),沿著CB方向勻速移動(dòng),速度為1cm/s;當(dāng)△PNM停止平移時(shí),
點(diǎn)Q也停止移動(dòng),如圖②.設(shè)移動(dòng)時(shí)間為t (s)(0<t<4).連接PQ、MQ、MC.解答下列問(wèn)題:
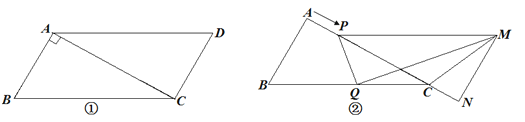
(1)當(dāng)t為何值時(shí),PQ∥MN?
(2)設(shè)△QMC的面積為y(cm2),求y與t之間的函數(shù)關(guān)系式;
(3)是否存在某一時(shí)刻t,使![]() ?若存在,求出t的值;若不存在,請(qǐng)說(shuō)明理由;
?若存在,求出t的值;若不存在,請(qǐng)說(shuō)明理由;
(4)是否存在某一時(shí)刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,請(qǐng)說(shuō)明理由.
【答案】![]()
![]() ;
;![]()
![]() ;
;![]() S△QMC:
S△QMC:![]() ;
;![]()
![]() .
.
【解析】
試題分析:![]() 當(dāng)PQ∥MN時(shí),可得:
當(dāng)PQ∥MN時(shí),可得:![]() ,從而得到:
,從而得到:![]() ,解方程求出
,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,則可以得到
,則可以得到![]() ,根據(jù)相似三角形的性質(zhì)可以求出
,根據(jù)相似三角形的性質(zhì)可以求出![]() ,
,![]() ,利用三角形的面積公式求出
,利用三角形的面積公式求出![]() 與
與![]() 的關(guān)系式;
的關(guān)系式;
![]() 根據(jù)S△QMC:
根據(jù)S△QMC:![]() 可以得到關(guān)于
可以得到關(guān)于![]() 的方程,解方程求出
的方程,解方程求出![]() 的值;
的值;
![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,則△CPD∽△CBA,利用相似三角形的性質(zhì)可以得到:
,則△CPD∽△CBA,利用相似三角形的性質(zhì)可以得到:![]()
![]() ,解方程求出
,解方程求出![]() 的值.
的值.
試題解析:(1)如圖所示,
若PQ∥MN,則有![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
解得![]() .
.
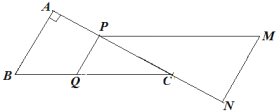
(2)如圖所示,
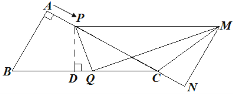
作![]() 于點(diǎn)
于點(diǎn)![]() ,則△CPD∽△CBA,
,則△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
又∵![]() ,
,
∴△QMC的面積為:![]()
(3)存在![]() 時(shí),使得S△QMC:
時(shí),使得S△QMC:![]() .
.
理由如下:
∵PM∥BC
∴![]()
∵S△QMC:![]() ,
,
∴S△PQC: S△ABC=1:5,
∵![]()
.∴![]()
∴![]()
∴![]()
∴存在當(dāng)![]() 時(shí),S△QMC:
時(shí),S△QMC:![]() ;
;
(4)存在某一時(shí)刻![]() ,使
,使![]() .
.
理由如下:
如圖所示,
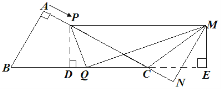
作![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,則△CPD∽△CBA,
,則△CPD∽△CBA,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵PQ⊥MQ,
∴△PDQ∽△QEM,
∴![]() ,
,
即![]()
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]()
![]() ,
,
即![]() ,
,
∴![]() ,
,![]() (舍去)
(舍去)
∴當(dāng)![]() 時(shí),使PQ⊥MQ.
時(shí),使PQ⊥MQ.


 小天才課時(shí)作業(yè)系列答案
小天才課時(shí)作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿(mǎn)分沖刺微測(cè)驗(yàn)系列答案
黃岡小狀元滿(mǎn)分沖刺微測(cè)驗(yàn)系列答案 新輔教導(dǎo)學(xué)系列答案
新輔教導(dǎo)學(xué)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】“建設(shè)大美青海,創(chuàng)建文明城市”,西寧市加快了郊區(qū)舊房拆遷的步伐.為了解被拆遷的236戶(hù)家庭對(duì)拆遷補(bǔ)償方案是否滿(mǎn)意,小明利用周末調(diào)查了其中的50戶(hù)家庭,有32戶(hù)對(duì)方案表示滿(mǎn)意.在這一抽樣調(diào)查中,樣本容量為
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】將一個(gè)正方體沿著某些棱剪開(kāi),展成一個(gè)平面圖形,至少需要剪的棱的條數(shù)是( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列事件是必然事件的為( )
A.明天太陽(yáng)從西方升起
B.?dāng)S一枚硬幣,正面朝上
C.打開(kāi)電視機(jī),正在播放“河池新聞”
D.任意一個(gè)三角形,它的內(nèi)角和等于180°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某車(chē)間有16名工人,每人每天可加工甲種零件5個(gè)或乙種零件4個(gè).在這16名工人中,一部分人加工甲種零件,其余的加工乙種零件.已知每加工一個(gè)甲種零件可獲利16元,每加工一個(gè)乙種零件可獲利24元.若此車(chē)間一共獲利1 440元,求這一天有幾名工人加工甲種零件.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是過(guò)A的一條直線(xiàn), 且B、C在AE的異側(cè), BD⊥AE于D, CE⊥AE于E.

(1)求證: BD=DE+CE.
(2)若直線(xiàn)AE繞A點(diǎn)旋轉(zhuǎn)到圖②位置時(shí)(BD<CE), 其余條件不變, 問(wèn)BD與DE、CE的數(shù)量關(guān)系如何? 請(qǐng)給予證明;
(3)若直線(xiàn)AE繞A點(diǎn)旋轉(zhuǎn)到圖③位置時(shí)(BD>CE), 其余條件不變, 問(wèn)BD與DE、CE的數(shù)量關(guān)系如何? 請(qǐng)直接寫(xiě)出結(jié)果, 不需證明.
(4)根據(jù)以上的討論,請(qǐng)用簡(jiǎn)潔的語(yǔ)言表達(dá)BD與DE,CE的數(shù)量關(guān)系。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有一組等式:12+22+22=32,22+32+62=72,32+42+122=132,42+52+202=212…請(qǐng)觀察它們的構(gòu)成規(guī)律,用你發(fā)現(xiàn)的規(guī)律寫(xiě)出第8個(gè)等式為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
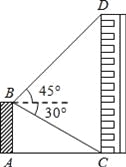
【題目】如圖,平臺(tái)AB高為12m,在B處測(cè)得樓房CD頂部點(diǎn)D的仰角為45°,底部點(diǎn)C的俯角為30°,求樓房CD的高度(![]() =1.7).
=1.7).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com