
【題目】如圖(1),![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于
于![]() ,過
,過![]() 點作與
點作與![]() 垂直的直線
垂直的直線![]() .動點
.動點![]() 從點
從點![]() 出發沿折線
出發沿折線![]() 以每秒1個單位長度的速度向終點
以每秒1個單位長度的速度向終點![]() 運動,運動時間為
運動,運動時間為![]() 秒,同時動點
秒,同時動點![]() 從點
從點![]() 出發沿折線
出發沿折線![]() 以相同的速度運動,當點
以相同的速度運動,當點![]() 到達點
到達點![]() 時
時![]() 、
、![]() 同時停止運動.
同時停止運動.


(1)請寫出![]() 的長為_______,
的長為_______,![]() 的長為_______;
的長為_______;
(2)當![]() 在
在![]() 上
上![]() 在
在![]() 上運動時,如圖(2),設
上運動時,如圖(2),設![]() 與
與![]() 交于點
交于點![]() ,當
,當![]() 為何值時,
為何值時,![]() 為等腰三角形?求出所有滿足條件的
為等腰三角形?求出所有滿足條件的![]() 值.
值.
【答案】(1)OC=2,BC=2;(2)t= ![]() 或
或![]()
【解析】
(1)求出∠B,根據直角三角形性質求出OA,求出AB,在△AOC中,根據勾股定理得出關于OC的方程,求出OC,即可得出答案;
(2)有三種情況:①OM=PM時,求出OP=2OQ,代入求出即可;②PM=OP時,此時不存在等腰三角形;③OM=OP時,過P作PG⊥ON于G,求出OG和QG的值,代入OG+QG=t2,即可求出答案.
(1)解:∵∠A=90°,∠AOB=60°,OB=2![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于
于![]() ,
,
∴∠B=30°,
∴OA=![]()
由勾股定理得:AB=3,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°=∠B,
∴OC=BC,
在△AOC中,AO2+AC2=CO2,
∴(![]() )2+(3OC)2=OC2,
)2+(3OC)2=OC2,
∴OC=2=BC,
答:OC=2,BC=2.
(2)解:如圖,∵ON⊥OB,

∴∠NOB=90°,
∵∠B=30°,∠A=90°,
∴∠AOB=60°,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°,
∴∠NOC=90°30°=60°,
①OM=PM時,
∠MOP=∠MPO=30°,
∴∠PQO=180°∠QOP∠MPO=90°,
∴OP=2OQ,
∴2(t2)=4t,
解得:t=![]()
②PM=OP時,
此時∠PMO=∠MOP=30°,
∴∠MPO=120°,
∵∠QOP=60°,
∴此時不存在;
③OM=OP時,
過P作PG⊥ON于G,
OP=4t,∠QOP=60°,
∴∠OPG=30°,
∴GO=![]() (4t),PG=
(4t),PG=![]() (4t),
(4t),
∵∠AOC=30°,OM=OP,
∴∠OPM=∠OMP=75°,
∴∠PQO=180°∠QOP∠QPO=45°,
∴PG=QG=![]() (4t),
(4t),
∵OG+QG=OQ,
∴![]() (4t)+
(4t)+![]() (4t)=t2,
(4t)=t2,
解得:t=![]()
綜合上述:當t為 ![]() 或
或![]() 時△OPM是等腰三角形.
時△OPM是等腰三角形.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:初中數學 來源: 題型:
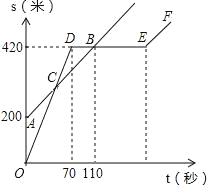
【題目】巴蜀中學的小明和朱老師一起到一條筆直的跑道上鍛煉身體,到達起點后小明做了一會準備活動,朱老師先跑.當小明出發時,朱老師已經距起點200米了.他們距起點的距離s(米)與小明出發的時間t(秒)之間的關系如圖所示(不完整).據圖中給出的信息,解答下列問題:
(1)在上述變化過程中,自變量是______,因變量是______;
(2)朱老師的速度為_____米/秒,小明的速度為______米/秒;
(3)當小明第一次追上朱老師時,求小明距起點的距離是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,AB∥OC,A(0,3),B(a,b),C(c,0),且a,c滿足![]() .點P從點A出發,以每秒1個單位長度的速度向點B運動,點Q從點O同時出發,以每秒2個單位長度的速度向點C運動,當點Q到達點C時,點P隨之停止運動.設運動時間為t(秒).
.點P從點A出發,以每秒1個單位長度的速度向點B運動,點Q從點O同時出發,以每秒2個單位長度的速度向點C運動,當點Q到達點C時,點P隨之停止運動.設運動時間為t(秒).

(1)B,C兩點的坐標為:B ,C ;
(2)當t為何值時,四邊形PQCB是平行四邊形?
(3)D為線段AB的中點,求當t為何值時,△ADQ是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校把一塊三角形的廢地開辟為動物園,如圖所示,測得AC=80m,BC=60m,AB=100m.
(1)若入口E在邊AB上,且與A、B等距離,求入口E到出口C的最短距離;
(2)若線段CD是一條小渠,且點D在邊AB上.點D距點A多遠時,水渠的距離最短?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】紅旗連鎖超市準備購進甲、乙兩種綠色袋裝食品.甲、乙兩種綠色袋裝食品的進價和售價如表.已知:用2000元購進甲種袋裝食品的數量與用1600元購進乙種袋裝食品的數量相同.
甲 | 乙 | |
進價(元/袋) |
|
|
售價(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使購進的甲、乙兩種綠色袋裝食品共800袋的總利潤(利潤=售價-進價)不少于4800元,且不超過4900元,問該超市有幾種進貨方案?
(3)在(2)的條件下,該超市如果對甲種袋裝食品每袋優惠![]() 元出售,乙種袋裝食品價格不變.那么該超市要獲得最大利潤應如何進貨?
元出售,乙種袋裝食品價格不變.那么該超市要獲得最大利潤應如何進貨?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l:y=﹣3x+3與x軸、y軸分別相交于A、B兩點,拋物線y=ax2﹣2ax+a+4(a<0)經過點B.

(1)求a的值,并寫出拋物線的表達式;
(2)已知點M是拋物線上的一個動點,并且點M在第一象限內,連接AM、BM,
①當點M(2,n)時,求n,并求△ABM的面積.
②當點M的橫坐標為m,△ABM的面積為S,求S與m的函數表達式,并求出S的最大值和此時點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】整體思想就是通過研究問題的整體形式從面對問題進行整體處理的解題方法.如 ,此題設“
,此題設“![]() ,
,![]() ”,得方程
”,得方程![]() ,解得
,解得![]() ,
,![]() .利用整體思想解決問題:采采家準備裝修-廚房,若甲,乙兩個裝修公司,合做
.利用整體思想解決問題:采采家準備裝修-廚房,若甲,乙兩個裝修公司,合做![]() 需周完成,甲公司單獨做4周后,剩下的由乙公司來做,還需
需周完成,甲公司單獨做4周后,剩下的由乙公司來做,還需![]() 周才能完成,設甲公司單獨完成需
周才能完成,設甲公司單獨完成需![]() 周,乙公司單獨完成需
周,乙公司單獨完成需![]() 周,則得到方程_______.利用整體思想 ,解得__________.
周,則得到方程_______.利用整體思想 ,解得__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分8分)某商家預測一種應季襯衫能暢銷市場,就用13200元購進了一批這種襯衫,面市后果然供不應求.商家又用28800元購進了第二批這種襯衫,所購數量是第一批購進量的2倍,但單價貴了10元.
(1)該商家購進的第一批襯衫是多少件?
(2)若兩批襯衫按相同的標價銷售,最后剩下50件按八折優惠賣出,如果兩批襯衫全部售完后利潤率不低于25%(不考慮其它因素),那么每件襯衫的標價至少是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com