
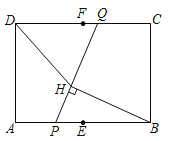
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 邊的中點(diǎn).動(dòng)點(diǎn)
邊的中點(diǎn).動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 向點(diǎn)
向點(diǎn)![]() 運(yùn)動(dòng),同時(shí),動(dòng)點(diǎn)
運(yùn)動(dòng),同時(shí),動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 向點(diǎn)
向點(diǎn)![]() 運(yùn)動(dòng),連接
運(yùn)動(dòng),連接![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() .若點(diǎn)
.若點(diǎn)![]() 的速度是點(diǎn)
的速度是點(diǎn)![]() 的速度的2倍,在點(diǎn)
的速度的2倍,在點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 運(yùn)動(dòng)至點(diǎn)
運(yùn)動(dòng)至點(diǎn)![]() 的過程中,線段
的過程中,線段![]() 長(zhǎng)度的最大值為_________,線段
長(zhǎng)度的最大值為_________,線段![]() 長(zhǎng)度的最小值為_________.
長(zhǎng)度的最小值為_________.
【答案】![]()
![]()
【解析】
連接EF,則EF⊥AB,過點(diǎn)P作PG⊥CD于點(diǎn)G,如圖1,由于![]() ,而PG=3,所以當(dāng)GQ最大時(shí)PQ最大,由題意可得當(dāng)P、A重合時(shí)GQ最大,據(jù)此即可求出PQ的最大值;設(shè)EF與PQ交于點(diǎn)M,連接BM,取BM的中點(diǎn)O,連接HO,如圖2,易證△FQM∽△EPM,則根據(jù)相似三角形的性質(zhì)可得EM為定值2,于是BM的長(zhǎng)度可得,由∠BHM=∠BEM=90°可得B、E、H、M四點(diǎn)共圓,且圓心為點(diǎn)O,于是當(dāng)D、H、O三點(diǎn)共線時(shí),DH的長(zhǎng)度最小,最小值為DO-OH,為此只需連接DO,求出DO的長(zhǎng)即可,可過點(diǎn)O作ON⊥CD于點(diǎn)N,作OK⊥BC于點(diǎn)K,如圖3,構(gòu)建Rt△DON,利用勾股定理即可求出DO的長(zhǎng),進(jìn)而可得答案.
,而PG=3,所以當(dāng)GQ最大時(shí)PQ最大,由題意可得當(dāng)P、A重合時(shí)GQ最大,據(jù)此即可求出PQ的最大值;設(shè)EF與PQ交于點(diǎn)M,連接BM,取BM的中點(diǎn)O,連接HO,如圖2,易證△FQM∽△EPM,則根據(jù)相似三角形的性質(zhì)可得EM為定值2,于是BM的長(zhǎng)度可得,由∠BHM=∠BEM=90°可得B、E、H、M四點(diǎn)共圓,且圓心為點(diǎn)O,于是當(dāng)D、H、O三點(diǎn)共線時(shí),DH的長(zhǎng)度最小,最小值為DO-OH,為此只需連接DO,求出DO的長(zhǎng)即可,可過點(diǎn)O作ON⊥CD于點(diǎn)N,作OK⊥BC于點(diǎn)K,如圖3,構(gòu)建Rt△DON,利用勾股定理即可求出DO的長(zhǎng),進(jìn)而可得答案.
解:連接EF,則EF⊥AB,過點(diǎn)P作PG⊥CD于點(diǎn)G,如圖1,則PE=GF,PG=AD=3,
設(shè)FQ=t,則GF=PE=2t,GQ=3t,
在Rt△PGQ中,由勾股定理得:![]() ,
,
∴當(dāng)t最大即EP最大時(shí),PQ最大,
由題意知:當(dāng)點(diǎn)P、A重合時(shí),EP最大,此時(shí)EP=2,則t=1,
∴PQ的最大值=![]() ;
;
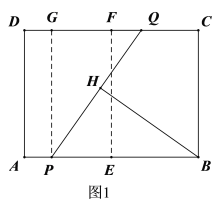
設(shè)EF與PQ交于點(diǎn)M,連接BM,取BM的中點(diǎn)O,連接HO,如圖2,
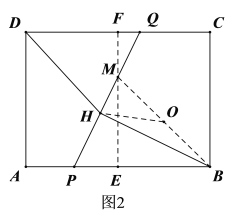
∵FQ∥PE,∴△FQM∽△EPM,
∴![]() ,
,
∵EF=3,
∴FM=1,ME=2,
∴![]() ,
,
∵∠BHM=∠BEM=90°,
∴B、E、H、M四點(diǎn)共圓,且圓心為點(diǎn)O,
∴![]() ,
,
∴當(dāng)D、H、O三點(diǎn)共線時(shí),DH的長(zhǎng)度最小,
連接DO,過點(diǎn)O作ON⊥CD于點(diǎn)N,作OK⊥BC于點(diǎn)K,如圖3,則OK=BK=1,
∴NO=2,CN=1,∴DN=3,
則在Rt△DON中,![]() ,
,
∴DH的最小值=DO-OH=![]() .
.
故答案為:![]() ,
,![]() .
.




| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩地之間有一條筆直的公路,小明從甲地出發(fā)步行前往乙地,同時(shí)小亮從乙地出發(fā)騎自行車前往甲地,小亮到達(dá)甲地沒有停留,按原路原速返回,追上小明后兩人一起步行到乙地.如圖,線段OA表示小明與甲地的距離y1(米)與行走的時(shí)間x(分鐘)之間的函數(shù)關(guān)系:折線BCDA表示小亮與甲地的距離y2(米)與行走的時(shí)間x(分鐘)之間的函數(shù)關(guān)系.請(qǐng)根據(jù)圖象解答下列問題:
(1)小明步行的速度是 米/分鐘,小亮騎自行車的速度是 米/分鐘;
(2)線段OA與BC相交于點(diǎn)E,求點(diǎn)E坐標(biāo);
(3)請(qǐng)直接寫出小亮從乙地出發(fā)到追上小明的過程中,與小明相距100米時(shí)x的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,點(diǎn)D是邊
,點(diǎn)D是邊![]() 的中點(diǎn),反比例函數(shù)
的中點(diǎn),反比例函數(shù)![]() 的圖象經(jīng)過點(diǎn)D,交
的圖象經(jīng)過點(diǎn)D,交![]() 邊于點(diǎn)E,直線
邊于點(diǎn)E,直線![]() 的解析式為
的解析式為![]() .
.

(1)求反比例函數(shù)![]() 的解析式和直線
的解析式和直線![]() 的解析式;
的解析式;
(2)在y軸上找一點(diǎn)P,使![]() 的周長(zhǎng)最小,求出此時(shí)點(diǎn)P的坐標(biāo);
的周長(zhǎng)最小,求出此時(shí)點(diǎn)P的坐標(biāo);
(3)在(2)的條件下,![]() 的周長(zhǎng)最小值是______.
的周長(zhǎng)最小值是______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
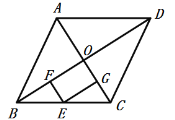
【題目】如圖,面積為S的菱形ABCD中,點(diǎn)O為對(duì)角線的交點(diǎn),點(diǎn)E是線段BC單位中點(diǎn),過點(diǎn)E作EF⊥BD于F,EG⊥AC與G,則四邊形EFOG的面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
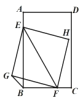
【題目】已知:矩形![]() 的邊
的邊![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿線段
出發(fā)沿線段![]() 向點(diǎn)
向點(diǎn)![]() 勻速運(yùn)動(dòng),點(diǎn)
勻速運(yùn)動(dòng),點(diǎn)![]() 同時(shí)從點(diǎn)
同時(shí)從點(diǎn)![]() 出發(fā)沿線段
出發(fā)沿線段![]() 向點(diǎn)
向點(diǎn)![]() 勻速運(yùn)動(dòng),速度均為
勻速運(yùn)動(dòng),速度均為![]() ,當(dāng)一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí)另一個(gè)點(diǎn)也停止運(yùn)動(dòng).連接
,當(dāng)一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí)另一個(gè)點(diǎn)也停止運(yùn)動(dòng).連接![]() ,以
,以![]() 為對(duì)角線作正方形
為對(duì)角線作正方形![]() ,連接
,連接![]() ,則
,則![]() 的長(zhǎng)度為____.
的長(zhǎng)度為____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
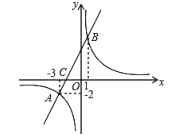
【題目】如圖,一次函數(shù)![]() 圖象與反比例函數(shù)
圖象與反比例函數(shù)![]() 的圖象交于點(diǎn)
的圖象交于點(diǎn)![]() 、
、![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
(1)求一次函數(shù)![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的解析式.
的解析式.
(2)求點(diǎn)![]() 坐標(biāo).
坐標(biāo).
(3)平面上的點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 、
、![]() 、
、![]() 構(gòu)成平行四邊形,請(qǐng)直接寫出滿足條件的
構(gòu)成平行四邊形,請(qǐng)直接寫出滿足條件的![]() 點(diǎn)坐標(biāo)______.
點(diǎn)坐標(biāo)______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某單位食堂為全體名職工提供了![]() 四種套餐,為了解職工對(duì)這四種套餐的喜好情況,單位隨機(jī)抽取
四種套餐,為了解職工對(duì)這四種套餐的喜好情況,單位隨機(jī)抽取![]() 名職工進(jìn)行“你最喜歡哪一種套餐(必選且只選一種)”問卷調(diào)查,根據(jù)調(diào)查結(jié)果繪制了條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖,部分信息如下:
名職工進(jìn)行“你最喜歡哪一種套餐(必選且只選一種)”問卷調(diào)查,根據(jù)調(diào)查結(jié)果繪制了條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖,部分信息如下:
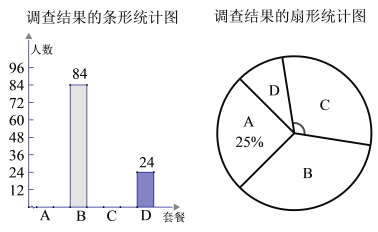
![]() 在抽取的
在抽取的![]() 人中最喜歡
人中最喜歡![]() 套餐的人數(shù)為 ,扇形統(tǒng)計(jì)圖中“
套餐的人數(shù)為 ,扇形統(tǒng)計(jì)圖中“![]() ”對(duì)應(yīng)扇形的圓心角的大小為 ;
”對(duì)應(yīng)扇形的圓心角的大小為 ;
![]() 依據(jù)本次調(diào)查的結(jié)果,估計(jì)全體
依據(jù)本次調(diào)查的結(jié)果,估計(jì)全體![]() 名職工中最喜歡
名職工中最喜歡![]() 套餐的人數(shù);
套餐的人數(shù);
![]() 現(xiàn)從甲、乙、丙、丁四名職工中任選兩人擔(dān)任“食品安全監(jiān)督員”,求甲被選到的概率.
現(xiàn)從甲、乙、丙、丁四名職工中任選兩人擔(dān)任“食品安全監(jiān)督員”,求甲被選到的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,A(t,0),B(t+4,0),線段AB的中點(diǎn)為C,若平面內(nèi)存在一點(diǎn)P使得∠APC或者∠BPC為直角(點(diǎn)P不與A,B,C重合),則稱P為線段AB的直角點(diǎn).
(1)當(dāng)t=0時(shí),
①在點(diǎn)P1(![]() ,0),P2(
,0),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )中,線段AB的直角點(diǎn)是 ;
)中,線段AB的直角點(diǎn)是 ;
②直線y=![]() x+b上存在四個(gè)線段AB的直角點(diǎn),直接寫出b取值范圍;
x+b上存在四個(gè)線段AB的直角點(diǎn),直接寫出b取值范圍;
(2)直線y=![]() x+1與x,y軸交于點(diǎn)M,N.若線段MN上只存在兩個(gè)線段AB的直角點(diǎn),直接寫出t取值范圍.
x+1與x,y軸交于點(diǎn)M,N.若線段MN上只存在兩個(gè)線段AB的直角點(diǎn),直接寫出t取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com