
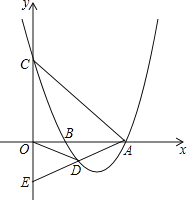
【題目】如圖,拋物線y=mx2-16mx+48m(m>0)與x軸交于A、B兩點(diǎn)(點(diǎn)B在點(diǎn)A左側(cè)),與y軸交于點(diǎn)C,點(diǎn)D是拋物線上的一個(gè)動(dòng)點(diǎn),且位于第四象限,連接OD、BD、AC、AD,延長(zhǎng)AD交y軸于點(diǎn)E.
(1)若△OAC為等腰直角三角形,求m的值.
(2)若對(duì)任意m>0,C、E兩點(diǎn)總關(guān)于原點(diǎn)對(duì)稱,求點(diǎn)D的坐標(biāo)(用含m的式子表示).
(3)當(dāng)點(diǎn)D運(yùn)動(dòng)到某一位置時(shí),恰好使得∠ODB=∠OAD,且點(diǎn)D為線段AE的中點(diǎn),此時(shí)對(duì)于該拋物線上任意一點(diǎn)P(x0,y0)總有n≥-4![]() my02-12
my02-12![]() y0-50成立,求實(shí)數(shù)n的最小值.
y0-50成立,求實(shí)數(shù)n的最小值.
【答案】(1)m=![]() ;(2)點(diǎn)D的坐標(biāo)為(8,-16m);(3)實(shí)數(shù)n的最小值為
;(2)點(diǎn)D的坐標(biāo)為(8,-16m);(3)實(shí)數(shù)n的最小值為![]()
【解析】
(1)根據(jù)y=mx2-16mx+48m=m(x-4)(x-12),可得A(12,0),C(0,48m),再根據(jù)OA=OC,即可得到12=48m,進(jìn)而得出m的值;
(2)根據(jù)C、E兩點(diǎn)總關(guān)于原點(diǎn)對(duì)稱,得到E(0,48m),根據(jù)E(0,48m),A(12,0)可得直線AE的解析式,最后解方程組即可得到直線AE與拋物線的交點(diǎn)D的坐標(biāo);
(3)根據(jù)△ODB∽△OAD,可得OD=4![]() ,進(jìn)而得到D(6,2
,進(jìn)而得到D(6,2![]() ),代入拋物線y=mx216mx+48m,求出m可得拋物線解析式,再根據(jù)點(diǎn)P(x0,y0)為拋物線上任意一點(diǎn),即可得出y0≥
),代入拋物線y=mx216mx+48m,求出m可得拋物線解析式,再根據(jù)點(diǎn)P(x0,y0)為拋物線上任意一點(diǎn),即可得出y0≥![]() ,令t=-4
,令t=-4![]() my02-12
my02-12![]() y0-50,求出t最大值=2(
y0-50,求出t最大值=2(![]() )2+4=
)2+4=![]() ,即可得實(shí)數(shù)n的最小值為
,即可得實(shí)數(shù)n的最小值為![]() .
.
解:(1)令y=mx2-16mx+48m=m(x-4)(x-12)=0,
則x1=12,x2=4,
∴A(12,0),即OA=12,
又∵C(0,48m),
∴當(dāng)△OAC為等腰直角三角形時(shí),OA=OC,即12=48m,
∴m=![]() ;.
;.
(2)由(1)可知點(diǎn)C(0,48m),
∵對(duì)任意m>0,C、E兩點(diǎn)總關(guān)于原點(diǎn)對(duì)稱,
∴必有E(0,-48m),
設(shè)直線AE的解析式為y=kx+b(k≠0),
將E(0,-48m),A(12,0)代入,可得![]() ,解得
,解得![]() ,
,
∴直線AE的解析式為y=4mx-48m,
∵點(diǎn)D為直線AE與拋物線的交點(diǎn),
∴解方程組![]() ,得
,得![]() 或
或![]() (舍去),
(舍去),
∴點(diǎn)D的坐標(biāo)為(8,-16m);
(3)當(dāng)∠ODB=∠OAD,∠DOB=∠AOD時(shí),△ODB∽△OAD,
∴![]() ,
,
∴OD2=OA×OB=12×4=48,
∴OD=4![]() ,
,
又∵點(diǎn)D為線段AE的中點(diǎn),
∴AE=2OD=8![]() ,
,
又∵OA=12,
∴OE=![]() =4
=4![]() ,
,
∴D(6,-2![]() ),
),
把D(6,-2![]() )代入拋物線y=mx2-16mx+48m,可得-2
)代入拋物線y=mx2-16mx+48m,可得-2![]() =36m-96m+48m,
=36m-96m+48m,
解得:m=![]() ,
,
∴拋物線的解析式為y=![]() (x-4)(x-12),即y=
(x-4)(x-12),即y=![]() (x-8)2-
(x-8)2-![]() ,
,
∵點(diǎn)P(x0,y0)為拋物線上任意一點(diǎn),
∴y0≥-![]() ,
,
令t=-4![]() my02-12
my02-12![]() y0-50=-2y02-12
y0-50=-2y02-12![]() y0-50=-2(y0+3
y0-50=-2(y0+3![]() )2+4,
)2+4,
則當(dāng)y0≥-![]() 時(shí),t最大值=-2(-
時(shí),t最大值=-2(-![]() +3
+3![]() )2+4=
)2+4=![]() ,
,
若要使n≥-4![]() my02-12
my02-12![]() y0-50成立,則n≥
y0-50成立,則n≥![]() ,
,
∴n≥![]() ,
,
∴實(shí)數(shù)n的最小值為![]() .
.


 浙江之星課時(shí)優(yōu)化作業(yè)系列答案
浙江之星課時(shí)優(yōu)化作業(yè)系列答案 激活思維優(yōu)加課堂系列答案
激活思維優(yōu)加課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某區(qū)各街道居民積極響應(yīng)“創(chuàng)文明社區(qū)”活動(dòng),據(jù)了解,某街道居民人口共有7.5萬(wàn)人,街道劃分為A,B兩個(gè)社區(qū),B社區(qū)居民人口數(shù)量不超過(guò)A社區(qū)居民人口數(shù)量的2倍.
(1)求A社區(qū)居民人口至少有多少萬(wàn)人?
(2)街道工作人員調(diào)查A,B兩個(gè)社區(qū)居民對(duì)“社會(huì)主義核心價(jià)值觀”知曉情況發(fā)現(xiàn):A社區(qū)有1.2萬(wàn)人知曉,B社區(qū)有1萬(wàn)人知曉,為了提高知曉率,街道工作人員用了兩個(gè)月的時(shí)間加強(qiáng)宣傳,A社區(qū)的知曉人數(shù)平均月增長(zhǎng)率為m%,B社區(qū)的知曉人數(shù)第一個(gè)月增長(zhǎng)了m%,第二個(gè)月增長(zhǎng)了2m%,兩個(gè)月后,街道居民的知曉率達(dá)到76%,求m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
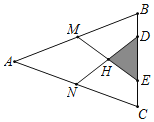
【題目】在△ABC中,AB=AC=13cm,BC=10cm,M、N分別是AB、AC的中點(diǎn),D、E在BC上,且DE=5cm,連結(jié)DN、ME交于H,則△HDE的面積為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,二次函數(shù)y=ax2+bx+c的圖象如圖所示,以下結(jié)論:①abc>0; ②b2-4ac<0 ; ③2a+b>0 ;④a+b+c>0,其中正確的個(gè)數(shù)( )
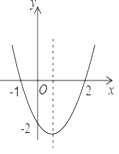
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,BC=6,E,F分別是AB,AC的中點(diǎn),動(dòng)點(diǎn)P在射線EF上,BP交CE于點(diǎn)D,∠CBP的平分線交CE于點(diǎn)Q,當(dāng)CQ=QE時(shí),EP+BP的值為( ).
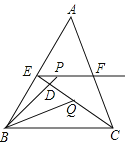
A.6B.9C.12D.18
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】自行車因其便捷環(huán)保深受人們喜愛(ài),成為日常短途代步與健身運(yùn)動(dòng)首選.如圖1是某品牌自行車的實(shí)物圖,圖2是它的簡(jiǎn)化示意圖.經(jīng)測(cè)量,車輪的直徑為66cm,車座B到地面的距離BE為90cm,中軸軸心C到地面的距離CF為33cm,車架中立管BC的長(zhǎng)為60cm,后輪切地面L于點(diǎn)D.(參考數(shù)據(jù):sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
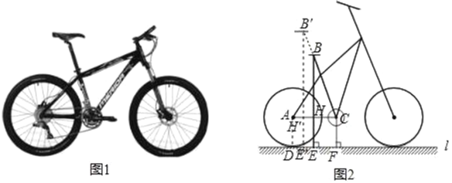
(1)求∠ACB的大小(精確到1°)
(2)如果希望車座B到地面的距離B'E′為96.8cm,車架中立管BC拉長(zhǎng)的長(zhǎng)度BB′應(yīng)是多少?(結(jié)果取整數(shù))
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在小水池旁有一盞路燈,已知支架AB的長(zhǎng)是0.8m,A端到地面的距離AC是4m,支架AB與燈柱AC的夾角為65°.小明在水池的外沿D測(cè)得支架B端的仰角是45°,在水池的內(nèi)沿E測(cè)得支架A端的仰角是50°(點(diǎn)C、E、D在同一直線上),求小水池的寬DE.(結(jié)果精確到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線y=ax2﹣4和y=﹣ax2+4都經(jīng)過(guò)x軸上的A、B兩點(diǎn),兩條拋物線的頂點(diǎn)分別為C、D.當(dāng)四邊形ACBD的面積為40時(shí),a的值為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某店代理某品牌商品的銷售.已知該品牌商品進(jìn)價(jià)每件40元,日銷售y(件)與銷售價(jià)x(元/件)之間的關(guān)系如圖所示(實(shí)線),付員工的工資每人每天100元,每天還應(yīng)支付其它費(fèi)用150元.

(1)求日銷售y(件)與銷售價(jià)x(元/件)之間的函數(shù)關(guān)系式;
(2)該店員工人共3人,若某天收支恰好平衡(收入=支出),求當(dāng)天的銷售價(jià)是多少?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com