【題目】在△ABC中，AB＝AC，AB的垂直平分線交AB于點D，交直線AC于點E，∠AEB＝80°，那么∠EBC等于（ ）
A. 15° B. 25° C. 15°或75° D. 25°或85°
科目：初中數學 來源： 題型：
【題目】已知實數x、y滿足2x+3y=1．
（1）用含有x的代數式表示y；
（2）若實數y滿足y＞1，求x的取值范圍；
（3）若實數x、y滿足x＞﹣1，y≥﹣
，且2x﹣3y=k，求k的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB=90°，AC=BC，△ABC的高CD與角平分線AE相交點F，過點C作CH⊥AE于G，交AB于H．下列說法：①∠BCH=∠CAE；②DF=EF；③CE=BH；④S△ABE=2S△ACE；⑤CF=
DF．正確的是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】先閱讀下面例題的解法，然后解答問題：
例：若多項式2x3-x2+m分解因式的結果中有因式2x+1，求實數m的值.
解：設2x3-x2+m=(2x+1)·A(A為整式).
若2x3-x2+m=(2x+1)·A=0，則2x+1=0或A=0.
由2x+1=0，解得x=-
.
∴x=-是方程2x3-x2+m=0的解. ∴2×(-)3-(-)2+m=0，即-
-+m=0. ∴m=.
(1)若多項式x2+px-6分解因式的結果中有因式x-3，則實數p= ；
(2)若多項式x3+5x2+7x+q分解因式的結果中有因式x+1，求實數q的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】從3，0，﹣1，﹣2，﹣3這五個數中，隨機抽取一個數，作為函數y=（5﹣m2）x和關于x的方程（m+1）x2+mx+1=0中m的值，恰好使所得函數的圖象經過第一、三象限，且方程有實數根的概率為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，點O是∠BCA與∠ABC的平分線的交點，過O作與BC平行的直線分別交AB、AC于D、E．已知△ABC的周長為15，BC的長為6，求△ADE的周長．
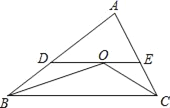
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知△ABC和△DCE均是等邊三角形，點 B、C、E 在同一條直線上，AE與 BD交于點 O，AE與 CD交于點 G，AC與 BD交于點 F，連接 OC、FG，則下列結論要：①AE＝BD；②AG＝BF；③FG∥BE；④OC 平分∠BOE，其中結論正確的個數有（ ）
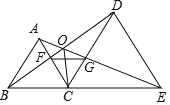
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，∠ABC＝∠ADC，BF、DE分別平分∠ABC與∠ADC．∠1＝∠3，求證：AB∥DC．
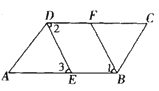
證明：∵∠ABC＝∠ADC ( )
∴
( )
∵BF、DE分別平分∠ABC與∠ADC ( )
∴
( )
∴∠______＝∠______ ( )
∵∠1＝∠3( )
∴∠2＝∠______ (等量代換)
∴____∥____ ( )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
