
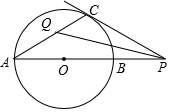
 如圖,P是⊙O的直線AB的延長線上的一點,PC與⊙O相切于點C,∠APC的角平分線交AC于點Q,則∠PQC=45°.
如圖,P是⊙O的直線AB的延長線上的一點,PC與⊙O相切于點C,∠APC的角平分線交AC于點Q,則∠PQC=45°. 分析 首先連接BC交PQ于E,由PC與圓D相切于點C,根據弦切角定理,即可得∠PCB=∠A,又由AB為直徑,即可得∠ACB=90°,然后由PQ平分∠APC與三角形外角的性質(∠CQP=∠A+∠APQ,∠CEQ=∠PCB+∠QPC),即可證得∠CQP=CEQ,則可求得∠PQC的度數.
解答 解:解:連接BC交PQ于E,
∵PC與圓D相切于點C,
∴∠PCB=∠A,
∵AB為直徑,
∴∠ACB=90°,
∵PQ平分∠APC,
∴∠APQ=∠QPC,
∵∠CQP=∠A+∠APQ,∠CEQ=∠PCB+∠QPC,
∴∠CQP=∠CEQ=$\frac{180°-90°}{2}$=45°.
故答案為45
點評 此題考查了圓的切線的性質,圓周角的性質,弦切角定理,等腰直角三角形的性質,以及三角形外角的性質等知識.此題綜合性較強,難度適中,解題的關鍵是注意數形結合思想的應用.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:選擇題
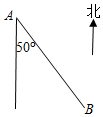 如圖,貨輪A與燈塔B相距20km,下列燈塔B相對于貨輪A的位置的描述中,正確的是( )
如圖,貨輪A與燈塔B相距20km,下列燈塔B相對于貨輪A的位置的描述中,正確的是( )| A. | 南偏東50° | B. | 南偏東50°且距貨輪20 km處 | ||
| C. | 距燈塔20 km處 | D. | 北偏西50°且距貨輪20 km處 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2ab2-2b2 | B. | 2a2b-2b3 | C. | 2ab2+2b2 | D. | 2ab-2ab2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
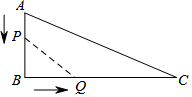 如圖,在△ABC中,∠B=90°,AB=12cm,BC=24cm,動點P從點A開始沿邊AB向B以2cm/s的速度移動,動點Q從點B開始沿BC邊向C以4cm/s的速度移動,如果P、Q分別從A、B同時出發,設運動時間為t,△PBQ的面積為S.
如圖,在△ABC中,∠B=90°,AB=12cm,BC=24cm,動點P從點A開始沿邊AB向B以2cm/s的速度移動,動點Q從點B開始沿BC邊向C以4cm/s的速度移動,如果P、Q分別從A、B同時出發,設運動時間為t,△PBQ的面積為S.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com