
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,
,![]() ,與
,與![]() 軸相交于點
軸相交于點![]() ,點
,點![]() 為拋物線的頂點,
為拋物線的頂點,![]() 軸于點
軸于點![]() ,且
,且![]() .
.

(1)求拋物線的解析式;
(2)做點![]() 與
與![]() 點關于對稱軸對稱,連接
點關于對稱軸對稱,連接![]() ,過點
,過點![]() 作
作![]() ,過點
,過點![]() 作
作![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,若
,若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在(2)的條件下,點![]() 是第一象限內拋物線上一點,連接
是第一象限內拋物線上一點,連接![]() 與
與![]() 相交于點
相交于點![]() ,過點
,過點![]() 做
做![]() 軸于點
軸于點![]() ,
,![]() 與
與![]() 相交于
相交于![]() ,連接
,連接![]() ,若
,若![]() ,求
,求![]() 點的坐標和
點的坐標和![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)首先根據拋物線解析式變換形式得出A、B兩點坐標,進而得出DE,再轉換成頂點式,即可得出拋物線解析式;
(2)根據對稱以及矩形的性質,通過等量互換,即可判定![]() ,進而得出F點坐標;
,進而得出F點坐標;
(3)首先通過等角互換得出![]() ,然后利用坐標構建方程即可得出點P坐標,再利用三角函數進行轉化即可得出
,然后利用坐標構建方程即可得出點P坐標,再利用三角函數進行轉化即可得出![]() 的值.
的值.
(1)∵![]() ,令
,令![]()
解![]() 得
得![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
解![]() 得
得![]()
∴![]() ;
;
(2)過![]() 作
作![]() 軸于
軸于![]() ,
,
∵![]() 、
、![]() 關于
關于![]() 對稱,
對稱,
∴![]() ,
,
∵四邊形![]() 為矩形,
為矩形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ;
;
(3)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
作![]() 交
交![]() 于
于![]() ,則
,則![]()
∴![]() ,
,

∴![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,
,
設![]() ,則
,則![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,![]() (舍去)
(舍去)
∴![]()
![]() 中:
中:![]()
![]() ,
,![]()
∵![]() ,
,
∴![]()
![]() 中:
中:![]() ,
, ,
,
![]()
![]() ,
,
作![]() 于
于![]() ,
,![]() 中:
中:![]() ,
,![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() 中:
中:![]()



 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的方程ax2+2x﹣3=0有兩個不相等的實數根.
(1)求a的取值范圍;
(2)若此方程的一個實數根為1,求a的值及方程的另一個實數根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,E為DC的中點,AD:AB=![]() :2,CP:BP=1:2,連接EP并延長,交AB的延長線于點F,AP、BE相交于點O.下列結論:①EP平分∠CEB;②
:2,CP:BP=1:2,連接EP并延長,交AB的延長線于點F,AP、BE相交于點O.下列結論:①EP平分∠CEB;②![]() =PBEF;③PFEF=2
=PBEF;③PFEF=2![]() ;④EFEP=4AOPO.其中正確的是( )
;④EFEP=4AOPO.其中正確的是( )
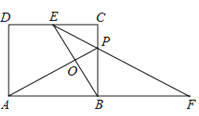
A. ①②③B. ①②④C. ①③④D. ③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“天空之城”摩天輪,位于寧波市杭州灣新區歡樂世界.摩天輪高約126米(最高點到地面的距離).如圖,點O是摩天輪的圓心,AB是其垂直于地面的直徑,小明在地面C處用測角儀測得摩天輪最高點A的仰角為45°,測得圓心O的仰角為30°,求摩天輪的半徑.(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
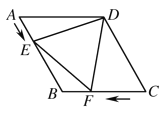
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,
,![]() 同時由
同時由![]() ,
,![]() 兩點出發,分別沿
兩點出發,分別沿![]() ,
,![]() 方向向點
方向向點![]() 勻速運動,點
勻速運動,點![]() 的運動速度為
的運動速度為![]() ,點
,點![]() 的運動速度為
的運動速度為![]() ,點
,點![]() 到達點
到達點![]() 后,點
后,點![]() 與點
與點![]() 同時停止運動.若運動時間為
同時停止運動.若運動時間為![]() 秒時,
秒時,![]() 為等邊三角形,則
為等邊三角形,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校初二學生每周上網的時間,兩位學生進行了抽樣調查.小麗調查了初二電腦愛好者中40名學生每周上網的時間;小杰從全校400名初二學生中隨機抽取了40名學生,調查了每周上網的時間.小麗與小杰整理各自樣本數據,如下表所示:
時間段 (小時/周) | 小麗抽樣 人數 | 小杰抽樣 人數 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每組可含最低值,不含最高值)

(1)你認為哪位同學抽取的樣本不合理?請說明理由;
(2)根據合理抽取的樣本,把上圖中的頻數分布直方圖補畫完整;
(3)專家建議每周上網2小時以上(含2小時)的同學應適當減少上網的時間,估計該校全體初二學生中有多少名同學應適當減少上網的時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,平行四邊形ABOC如圖放置,點A、C的坐標分別是為(0,3)、(-1,0),將此平行四邊形繞點O順時針旋轉90°,得到平行四邊形A′B′OC′.

(1)若拋物線過點C、A、A′,求此拋物線的解析式;
(2)求平行四邊形ABOC和平行四邊形A′B′OC′重疊部分△OC′D的周長;
(3)點M是第一象限內拋物線上的一動點,問:點M在何處時;△AMA′的面積最大?最大面積是多少?并求出此時點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx﹣3的圖象經過點(1,﹣4)和(﹣1,0).
(1)求這個二次函數的表達式;
(2)x在什么范圍內,y隨x增大而減小?該函數有最大值還是有最小值?求出這個最值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com