
【題目】如圖,⊙O過點B、C,圓心O在等腰直角三角形ABC的內部,∠BAC=90°,OA=1,BC=6,則⊙O的半徑為( ) 
A.6
B.13
C.![]()
D.2 ![]()
【答案】C
【解析】解:過O作OD⊥BC, ∵BC是⊙O的一條弦,且BC=6,
∴BD=CD= ![]() BC=
BC= ![]() ×6=3,
×6=3,
∴OD垂直平分BC,又AB=AC,
∴點A在BC的垂直平分線上,即A,O、D三點共線,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∴△ABD也是等腰直角三角形,
∴AD=BD=3,
∵OA=1,
∴OD=AD﹣OA=3﹣1=2,
在Rt△OBD中,
OB= ![]() =
= ![]() =
= ![]()
故選C.
過O作OD⊥BC,由垂徑定理可知BD=CD= ![]() BC,根據△ABC是等腰直角三角形可知∠ABC=45°,故△ABD也是等腰直角三角形,BD=AD,再由OA=1可求出OD的長,在Rt△OBD中利用勾股定理即可求出OB的長.
BC,根據△ABC是等腰直角三角形可知∠ABC=45°,故△ABD也是等腰直角三角形,BD=AD,再由OA=1可求出OD的長,在Rt△OBD中利用勾股定理即可求出OB的長.


科目:初中數學 來源: 題型:
【題目】如圖,CB=CA,∠ACB=90°,點D在邊BC上(與B、C不重合),四邊形ADEF為正方形,過點F作FG⊥CA,交CA的延長線于點G,連接FB,交DE于點Q,給出以下結論:
①AC=FG;②S△FAB:S四邊形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正確的結論的個數是( )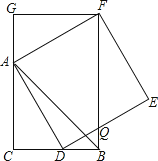
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七巧板是我們祖先的一項卓越創造,被譽為“東方魔板”,小明利用七巧板(如圖1所示)中各板塊的邊長之間的關系拼成一個凸六邊形(如圖2所示),則該凸六邊形的周長是cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AD是角平分線,BE平分∠ABC交AD于點E,點O在AB上,以OB為半徑的⊙O經過點E,交AB于點F 
(1)求證:AD是⊙O的切線;
(2)若AC=4,∠C=30°,求 ![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB、CD相交于點O,OE⊥CD,OF平分∠BOD. 
(1)圖中除直角外,請寫出一對相等的角嗎:(寫出符合的一對即可)
(2)如果∠AOE=26°,求∠BOD和∠COF的度數.(所求的角均小于平角)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某貨站傳送貨物的平面示意圖.為了提高傳送過程的安全性,工人師傅欲減小傳送帶與地面的夾角,使其由45°改為30°.已知原傳送帶AB長為4米. 
(1)求新傳送帶AC的長度;
(2)如果需要在貨物著地點C的左側留出2米的通道,試判斷距離B點4米的貨物MNQP是否需要挪走,并說明理由.(說明:(1)(2)的計算結果精確到0.1米,參考數據: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.24,
≈2.24, ![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】函數y=x2+bx+c與y=x的圖象如圖所示,有以下結論: ①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④當1<x<3時,x2+(b﹣1)x+c<0.
其中正確的個數為( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年1月,市教育局在全市中小學中選取了63所學校從學生的思想品德、學業水平、學業負擔、身心發展和興趣特長五個維度進行了綜合評價.評價小組在選取的某中學七年級全體學生中隨機抽取了若干名學生進行問卷調查,了解他們每天在課外用于學習的時間,并繪制成如下不完整的統計圖.
根據上述信息,解答下列問題:
(1)本次抽取的學生人數是;扇形統計圖中的圓心角α等于;補全統計直方圖;
(2)被抽取的學生還要進行一次50米跑測試,每5人一組進行.在隨機分組時,小紅、小花兩名女生被分到同一個小組,請用列表法或畫樹狀圖求出她倆在抽道次時抽在相鄰兩道的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】多多班長統計去年1~8月“書香校園”活動中全班同學的課外閱讀數量(單位:本),繪制了如圖折線統計圖,下列說法正確的是( ) 
A.極差是47
B.眾數是42
C.中位數是58
D.每月閱讀數量超過40的有4個月
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com