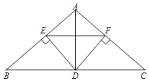
【題目】如圖，在
中，
，
是邊
上一點，
，
，垂足分別是
、
，
．
求證：
；
若
，求證：四邊形
是正方形．
【答案】證明見解析
【解析】
（1）根據相似三角形的性質得到
=
，根據AB=AC，得到AE=AF，利用HL定理證明；
（2）根據等腰三角形的性質得到BC=2BD，得到BD=AD，根據正方形的判定定理即可證明．
（1）∵△AEF∽△ABC，∴=．
∵AB=AC，∴AE=AF．
∵DE⊥AB，DF⊥AC，∴∠AED=∠AFD=90°．在Rt△AED和Rt△AFD中，∵
，∴Rt△AED≌Rt△AFD；
（2）∵Rt△AED≌Rt△AFD，∴∠EAD=∠FAD．
∵AB=AC，∴AD⊥BC，BC=2BD．
∵BC=2AD，∴BD=AD．
∵AD⊥BC，∴∠ADB=90°，∴∠B=∠BAD=45°，∴∠BAC=2∠BAD=90°．
∵∠AED=∠AFD=90°，∴四邊形AEDF是矩形．
∵AE=AF，∴矩形AEDF是正方形．
科目：初中數學 來源： 題型：
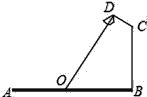
【題目】如圖，要在寬AB為20米的甌海大道兩邊安裝路燈，路燈的燈臂CD與燈柱BC成120°角，燈罩的軸線DO與燈臂CD垂直，當燈罩的軸線DO通過公路路面的中心線（即O為AB的中點）時照明效果最佳，若CD=
米，則路燈的燈柱BC高度應該設計為____米（計算結果保留根號）．
查看答案和解析>>
科目：初中數學 來源： 題型：
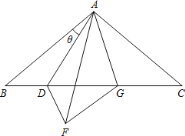
【題目】在ABC 中， AB AC ， BAC=100°，點 D 在 BC 上， ABD 和AFD 關于直線 AD 對稱， FAC 的平分線交 BC 于點 G，連接 FG 當BAD _________.時，DFG為等腰三角形.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知AB是⊙O的直徑，弦CD⊥AB于H，過CD延長線上一點E作⊙O的切線交AB的延長線于F，切點為G，連接AG交CD于K．
（1）如圖1，求證：KE=GE；
（2）如圖2，連接CABG，若∠FGB=
∠ACH，求證：CA∥FE；
（3）如圖3，在（2）的條件下，連接CG交AB于點N，若sinE=
，AK=
，求CN的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y=x2
2x+c的頂點A在直線l：y=x
5上．
（1）求拋物線頂點A的坐標；
（2）設拋物線與y軸交于點B，與x軸交于點C、D（C點在D點的左側），試判斷△ABD的形狀；
（3）在直線l上是否存在一點P，使以點P、A、B、D為頂點的四邊形是平行四邊形？若存在，求點P的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】發現與探索
小麗發現通過用兩種不同的方法計算同一幾何體體積，就可以得到一個恒等式.如圖是邊長為
的正方體，被如圖所示的分割線分成
塊.
；
；
用不同的方法計算這個正方體的體積，就可以得到一個等式，這個等式為：________；
已知
，
，利用上面的規律求
的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把大小和形狀完全相同的
張卡片分成兩組，每組
張，分別標上
、
、，將這兩組卡片分別放入兩個盒子中攪勻，再從中隨機抽取一張．
請用畫樹狀圖的方法求取出的兩張卡片數字之和為奇數的概率；
若取出的兩張卡片數字之和為奇數，則甲勝；取出的兩張卡片數字之和為偶數，則乙勝；試分析這個游戲是否公平？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小紅的父母開了一個小服裝店，出售某種進價為
元的服裝，現每件
元，每星期可賣
件．該同學對市場作了如下調查：每降價
元，每星期可多賣
件；每漲價元，每星期要少賣
件．
小紅已經求出在漲價情況下一個星期的利潤
（元）與售價
（元）（為整數）的函數關系式為
，請你求出在降價的情況下與的函數關系式；
在降價的條件下，問每件商品的售價定為多少時，一個星期的利潤恰好為
元？
問如何定價，才能使一星期獲得的利潤最大？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
