
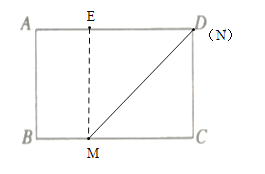
【題目】如圖1 ,在矩形紙片![]() 中,
中,![]() ,折疊紙片使
,折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]()
![]() 求證:四邊形
求證:四邊形![]() 為菱形;
為菱形;
![]() 當點
當點![]() 在
在![]() 邊上移動時,折痕的端點
邊上移動時,折痕的端點![]() 也隨之移動,若限定
也隨之移動,若限定![]() 分別在邊
分別在邊![]() .上移動,求出點
.上移動,求出點![]() 在邊
在邊![]() 上移動的最大距離.
上移動的最大距離.

【答案】(1)見詳解;(2)2.
【解析】
(1)根據折疊的性質得出![]() ;再根據平行的性質及等角對等邊得出
;再根據平行的性質及等角對等邊得出![]() 即可得證;
即可得證;
(2)根據正方形的性質,對稱的性質以及勾股定理即可得出AE的值,從而得出DE的值;當點B與點M 重合時,點D離點E最近,此時DE=1cm,當點N與點C重合時,點D離點E最遠,此時四邊形EMCD為正方形,DE=DC=3cm,即可得出答案.
(1)![]() 折疊紙片使
折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() ,
,
![]() 點C與點E關于MN對稱
點C與點E關于MN對稱
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四邊形
四邊形![]() 為菱形;
為菱形;
(2)![]() 四邊形ABCD為矩形
四邊形ABCD為矩形
![]()
![]() C、E關于MN對稱
C、E關于MN對稱
![]()
在![]() 中,
中,![]()
![]()
![]()
當點B與點M 重合時,點D離點E最近,DE=1cm
當點N與點C重合時,點D離點E最遠
此時四邊形EMCD為正方形,DE=DC=3cm
![]() 點E在AD邊上移動最大距離為2cm.
點E在AD邊上移動最大距離為2cm.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(a,0),C(b,2),且滿足(a+b)2+|a-b+4|=0,過點C作CB⊥x軸于B.
(1)如圖1,求△ABC的面積.
(2)如圖2,若過B作BD∥AC交y軸于D,在△ABC內有一點E,連接AE.DE,若∠CAE+∠BDE=∠EAO+∠EDO,求∠AED的度數.
(3)如圖3,在(2)的條件下,DE與x軸交于點M,AC與y軸交于點F,作△AME的角平分線MP,在PE上有一點Q,連接QM,∠EAM+2∠PMQ=45°,當AE=2AM,FO=2QM時,求點E的縱坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了讓市民享受到更多的優惠,相關部門擬確定一個折扣線,計劃使50%左右的人獲得折扣優惠.某市針對乘坐地鐵的人群進行了調查.調查小組在各地鐵站隨機調查了該市1000人上一年乘坐地鐵的月均花費(單位:元),繪制了頻數分布直方圖,如圖所示.下列說法正確的是( )

①每人乘坐地鐵的月均花費最集中的區域在80~100元范圍內;
②每人乘坐地鐵的月均花費的平均數范圍是40~60元范圍內;
③每人乘坐地鐵的月均花費的中位數在60~100元范圍內;
④乘坐地鐵的月均花費達到80元以上的人可以享受折扣.
A.①②④B.①③④C.③④D.①②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市銷售櫻桃,已知櫻桃的進價為15元/千克,如果售價為20元/千克,那么每天可售出250千克,如果售價為25元/千克,那么每天可獲利2000元,經調查發現:每天的銷售量y(千克)與售價x(元/千克)之間存在一次函數關系.
(1)求y與x之間的函數關系式;
(2)若櫻桃的售價不得高于28元/千克,請問售價定為多少時,該超市每天銷售櫻桃所獲的利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l1∥l2,直線l3和直線l1,l2交于C、D兩點,點P在直線CD上.
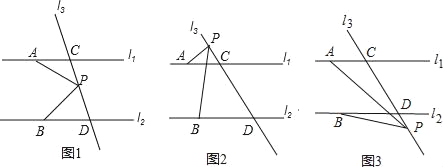
(1)試寫出圖1中∠APB、∠PAC、∠PBD之間的關系,并說明理由;
(2)如果P點在C、D之間運動時,∠APB、∠PAC、∠PBD之間的關系會發生變化嗎?
答: (填發生或不發生)
(3)若點P在C、D兩點的外側運動時(P點與點C、D不重合),如圖2,圖3,試分別寫出∠PAC、∠APB、∠PBD之間的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 探究發現
探究發現
如圖1,正方形![]() 中,點
中,點![]() 分別在
分別在![]() 上,
上,![]() .通過探究可以發現線段
.通過探究可以發現線段![]() 和
和![]() 之間存在一定的數量關系:
之間存在一定的數量關系:

![]() 拓展延伸
拓展延伸
如圖2,正方形![]() 中,點
中,點![]() 分別在
分別在![]() 的延長線上,
的延長線上,![]()
①線段![]() 和
和![]() 之間有怎樣的數量關系?寫出猜想,并加以證明;
之間有怎樣的數量關系?寫出猜想,并加以證明;
②若![]() ,求
,求![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司為了更好治理污水質,改善環境,決定購買10臺污水處理設備,現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如表:
A型 | B型 | |
價格(萬元/臺) | a | b |
處理污水量(噸/月) | 200 | 160 |
經調查:購買一臺A型設備比購買一臺B型設備多3萬元,購買2臺A型設備比購買3臺B型設備少1萬元.
(1)求a,b的值;
(2)經預算:市治污公司購買污水處理設備的資金不超過78萬元,你認為該公司有哪幾種購買方案;
(3)在(2)間的條件下,若每月要求處理的污水量不低于1620噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點A(-1,0),頂點坐標為(1,n),與y軸的交點在(0,2),(0,3)之間(包含端點),則下列結論:①當
軸交于點A(-1,0),頂點坐標為(1,n),與y軸的交點在(0,2),(0,3)之間(包含端點),則下列結論:①當![]() 時,
時, ![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中,正確的是_______.
中,正確的是_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l3,l4與l1,l2分別相交于點A、B、C、D,且∠1+∠2=180°.
(1)直線l1與l2平行嗎?為什么?
(2)點E在線段AD上,∠ABE=30°,∠BEC=62°,求∠DCE的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com