
【題目】如圖,拋物線y=x2-4x與x軸交于O,A兩點,P為拋物線上一點,過點P的直線y=x+m與對稱軸交于點Q.

(1)這條拋物線的對稱軸是 ,直線PQ與x軸所夾銳角的度數是 ;
(2)若兩個三角形面積滿足S△POQ=![]() S△PAQ,求m的值;
S△PAQ,求m的值;
(3)當點P在x軸下方的拋物線上時,過點C(2,2)的直線AC與直線PQ交于點D,求:①PD+DQ的最大值;②PD![]() DQ的最大值.
DQ的最大值.
【答案】(1)x=2,45;(2)m=-1或2;(3)①6![]() ;②18.
;②18.
【解析】試題分析:(1)把解析式轉化成頂點式,或利用對稱軸公式即可得該拋物線的對稱軸,利用直線y=x+m與坐標軸的交點坐標即可求得直線PQ與x軸所夾銳角的度數;(2)分情況討論,即直線PQ與x軸的交點落在OA的延長線上,OA上,AO的延長線上三種情況討論m值.設直線PQ交x軸于點B,分別過O點,A點作PQ的垂線,垂足分別是E、F,,當點B在OA的延長線時,S△POQ=![]() S△PAQ不成立;當點B落在線段OA上時,
S△PAQ不成立;當點B落在線段OA上時, ![]() ,由△OBE∽△ABF得,
,由△OBE∽△ABF得, ![]() ,由對稱軸求出A點坐標,再由比例式求出B點坐標,代入直線PQ解析式,即可求得m值;當點B落在線段AO的延長線上時,同理由比例式求出B點坐標,進而確定m值;(3)①由題意可過點C作CH∥x軸交直線PQ于點H,可得△CHQ是等腰三角形,AD⊥PH,DQ=DH,PD+DQ=PH,過P點作PM⊥CH于點M,可得△PMH是等腰直角三角形,PH=
,由對稱軸求出A點坐標,再由比例式求出B點坐標,代入直線PQ解析式,即可求得m值;當點B落在線段AO的延長線上時,同理由比例式求出B點坐標,進而確定m值;(3)①由題意可過點C作CH∥x軸交直線PQ于點H,可得△CHQ是等腰三角形,AD⊥PH,DQ=DH,PD+DQ=PH,過P點作PM⊥CH于點M,可得△PMH是等腰直角三角形,PH=![]() PM,即當PM最大時,PH最大,顯然當點P在拋物線頂點處時,PM最大,此時PM=6,于是求得PH的最大值.即PD+DQ的最大值;②上題求得PD+DQ的最大值為6
PM,即當PM最大時,PH最大,顯然當點P在拋物線頂點處時,PM最大,此時PM=6,于是求得PH的最大值.即PD+DQ的最大值;②上題求得PD+DQ的最大值為6![]() .即PD+DQ ≤6
.即PD+DQ ≤6![]() ,設PD=a,則DQ ≤6
,設PD=a,則DQ ≤6![]() -a,所以PD
-a,所以PD![]() DQ≤a(6
DQ≤a(6![]() -a)=-(a-3
-a)=-(a-3![]() )2+18,即當PD=DQ=3
)2+18,即當PD=DQ=3![]() 時求得PD
時求得PD![]() DQ的最大值
DQ的最大值
試題解析:(1)∵y=x2-4x=(x-2)2-4,∴拋物線的對稱軸是直線x=2,∵直線y=x+m與坐標軸的交點坐標為(-m,0),(0,m),∴交點到原點的距離相等,∴直線與坐標軸圍成的三角形是等腰直角三角形,∴直線PQ與x軸所夾銳角的度數是45°.故答案為x=2;45°.(2)設直線PQ交x軸于點B,分別過O點,A點作PQ的垂線,垂足分別是E、F,顯然當點B在OA的延長線時,OE>AF,S△POQ=![]() S△PAQ不成立;①當點B落在線段OA上時,如圖①,
S△PAQ不成立;①當點B落在線段OA上時,如圖①,
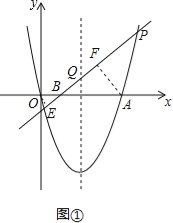
![]() ,由△OBE∽△ABF得,
,由△OBE∽△ABF得, ![]() ,∴AB=3OB,∴OB =
,∴AB=3OB,∴OB =![]() OA,由y=x2-4x得點A(4,0),∴OB=1,∴B(1,0),代入y=x+m,∴1+m=0,∴m=-1;②當點B落在線段AO的延長線上時,如圖②,
OA,由y=x2-4x得點A(4,0),∴OB=1,∴B(1,0),代入y=x+m,∴1+m=0,∴m=-1;②當點B落在線段AO的延長線上時,如圖②,

同理可得OB =![]() OA=2,∴B(-2,0),∴-2+m=0,∴m=2,;綜上所述,當m=-1或2時,S△POQ=
OA=2,∴B(-2,0),∴-2+m=0,∴m=2,;綜上所述,當m=-1或2時,S△POQ=![]() S△PAQ;
S△PAQ;
(3)①過點C作CH∥x軸交直線PQ于點H,如圖③,

可得△CHQ是等腰三角形,∵![]() =45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,過P點作PM⊥CH于點M,則△PMH是等腰直角三角形,∴PH=
=45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,過P點作PM⊥CH于點M,則△PMH是等腰直角三角形,∴PH=![]() PM,∴當PM最大時,PH最大,∴當點P在拋物線頂點處時,PM最大,此時PM=6,∴PH的最大值為6
PM,∴當PM最大時,PH最大,∴當點P在拋物線頂點處時,PM最大,此時PM=6,∴PH的最大值為6![]() ,即PD+DQ的最大值為6
,即PD+DQ的最大值為6![]() .②由①可知:PD+DQ ≤6
.②由①可知:PD+DQ ≤6![]() ,設PD=a,則DQ ≤6
,設PD=a,則DQ ≤6![]() -a,∴PD
-a,∴PD![]() DQ ≤a(6
DQ ≤a(6![]() -a)=-a2+6
-a)=-a2+6![]() a=-(a-3
a=-(a-3![]() )2+18,∵當點P在拋物線的頂點時,a=3
)2+18,∵當點P在拋物線的頂點時,a=3![]() ,∴PD
,∴PD![]() DQ ≤18.;∴PD
DQ ≤18.;∴PD![]() DQ的最大值為18.
DQ的最大值為18.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=1,BC=2,BC在x軸上,一次函數y=kx﹣2的圖象經過點A、C,并與y軸交于點E,反比例函數y=![]() 的圖象經過點A.
的圖象經過點A.

(1)點E的坐標是 ;
(2)求反比例函數的解析式;
(3)求當一次函數的值小于反比例函數的值時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中AD⊥BC,CE⊥AB,垂足分別為D、E,AD、CE交于點H,已知EH=EB=3,AE=4,則CH的長是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班數學興趣小組進行了如下探究:(1)如圖①,若四邊形ABCD是矩形,對角線AC、BD交點為P,過點P作PQ⊥BC于點Q,連結DQ交AC于點P1,過點P1作P1Q1⊥BC于點Q1,已知AB=CD=a,則PQ= ,P1Q1= .(用含a的代數式表示)
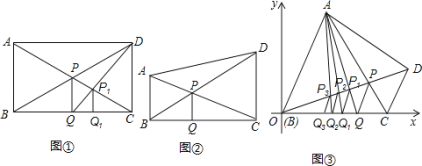
(2)如圖②,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AC、BD交于點P,過點P作PQ⊥BC于點Q.已知AB=a,CD=b,請用含a、b的代數式表示線段PQ的長,寫出你的解題過程.
(3)如圖③,在直角坐標系xOy中,梯形ABCD的腰BC在x軸正半軸上(點B與原點O重合),AB∥CD,∠ABC=60°,AC、BD交于點P,過點P作PQ∥CD交BC于點Q,連結AQ交BD于點P1,過點P1作P1Q1∥CD交BC于點Q1.連結AQ1交BD于點P2,過點P2作P2Q2∥CD交BC于點Q2,…,已知AB=a,CD=b,則點P1的縱坐標為 點Pn的縱坐標為 (直接用含a、b、n的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,AD垂直于過點C的切線,垂足為D.
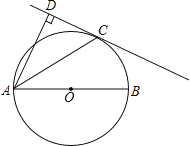
(1)求證:AC平分BAD;
(2)若AC=2![]() ,CD=2,求⊙O的直徑.
,CD=2,求⊙O的直徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法不正確的是( )
A. 各邊都相等的多邊形是正多邊形
B. 正多形的各邊都相等
C. 正三角形就是等邊三角形
D. 各內角相等的多邊形不一定是正多邊形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com