
【題目】如圖,△OAP是等腰直角三角形,∠OAP=90°,點A在第四象限,點P坐標為(8,0),拋物線y=ax2+bx+c經過原點O和A、P兩點.

(1)求拋物線的函數關系式.
(2)點B是y軸正半軸上一點,連接AB,過點B作AB的垂線交拋物線于C、D兩點,且BC=AB,求點B坐標;
(3)在(2)的條件下,點M是線段BC上一點,過點M作x軸的垂線交拋物線于點N,求△CBN面積的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根據![]() 是等腰直角三角形,
是等腰直角三角形,![]() 和點P的坐標求出點A的坐標,再利用待定系數法即可求得;
和點P的坐標求出點A的坐標,再利用待定系數法即可求得;
(2)設點![]() ,如圖(見解析),過點C作CH垂直y軸于點H,過點A作AQ垂直y軸于點Q,易證明
,如圖(見解析),過點C作CH垂直y軸于點H,過點A作AQ垂直y軸于點Q,易證明![]() ,可得
,可得![]() ,則點C坐標為
,則點C坐標為![]() ,將其代入題(1)中的拋物線函數關系式即可得;
,將其代入題(1)中的拋物線函數關系式即可得;
(3)如圖,延長NM交CH于點E,則![]() ,先通過點B、C求出直線BC的函數關系式,因點N在拋物線上,則設
,先通過點B、C求出直線BC的函數關系式,因點N在拋物線上,則設![]() ,則可得點M的坐標,再根據三角形的面積公式列出等式,利用二次函數的性質求最值即可.
,則可得點M的坐標,再根據三角形的面積公式列出等式,利用二次函數的性質求最值即可.
(1)![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,點P坐標為
,點P坐標為![]()
則點A的坐標為![]()
將點O、A、B三點坐標代入拋物線的函數關系式得:
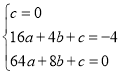 ,解得:
,解得: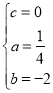
故拋物線的函數關系式為:![]() ;
;
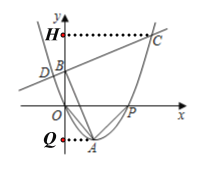
(2)設點![]() ,過點C作CH垂直y軸于點H,過點A作AQ垂直y軸于點Q,
,過點C作CH垂直y軸于點H,過點A作AQ垂直y軸于點Q,
![]()
![]()
又![]()
![]()
![]()
故點C的坐標為![]()
將點C的坐標代入題(1)的拋物線函數關系式得:
![]() ,解得:
,解得:![]()
故點B的坐標為![]() ;
;
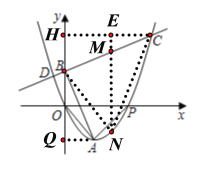
(3)如圖,延長NM交CH于點E,則![]()
設直線BC的解析式為:![]() ,將點
,將點![]() ,點
,點![]() 代入得:
代入得:
![]() 解得:
解得:![]()
則直線BC的解析式為:![]()
因點N在拋物線上,設![]() ,則點M的坐標為
,則點M的坐標為![]()
![]() 的面積
的面積![]()
即![]()
整理得:![]()
又因點M是線段BC上一點,則![]()
由二次函數的性質得:當![]() 時,y隨x的增大而增大;當
時,y隨x的增大而增大;當![]() 時,y隨x的增大而減小
時,y隨x的增大而減小
故當![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.


 一課一練課時達標系列答案
一課一練課時達標系列答案科目:初中數學 來源: 題型:
【題目】2019年5月,以“尋根國學,傳承文明”為主題的蘭州市第三屆“國學少年強一國學知識挑戰賽”總決賽拉開帷幕,小明晉級了總決賽.比賽過程分兩個環節,參賽選手須在每個環節中各選擇一道題目.
第一環節:寫字注音、成語故事、國學常識、成語接龍(分別用![]() 表示);
表示);
第二環節:成語聽寫、詩詞對句、經典通讀(分別用![]() 表示)
表示)
(1)請用樹狀圖或列表的方法表示小明參加總決賽抽取題目的所有可能結果
(2)求小明參加總決賽抽取題目都是成語題目(成語故事、成語接龍、成語聽寫)的概率。
查看答案和解析>>
科目:初中數學 來源: 題型:
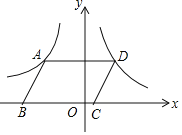
【題目】如圖,在平面直角坐標系中,ABCD的頂點B,C在x軸上,A,D兩點分別在反比例函數y=﹣![]() (x<0)與y=
(x<0)與y=![]() (x>0)的圖象上,若ABCD的面積為4,則k的值為:_____.
(x>0)的圖象上,若ABCD的面積為4,則k的值為:_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列條件中不能判定這兩個三角形相似的是( )
A. ∠A=55°,∠D=35°
B. AC=9,BC=12,DF=6,EF=8
C. AC=3,BC=4,DF=6,DE=8
D. AB=10,AC=8,DE=15,EF=9
查看答案和解析>>
科目:初中數學 來源: 題型:
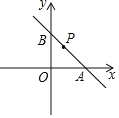
【題目】如圖,在平面直角坐標系中,已知,A(2![]() ,0),B(0,2),C(
,0),B(0,2),C(![]() ,0),點P(m,n)為直線AB上一動點,若∠OPC=30°,則m的值為_____.
,0),點P(m,n)為直線AB上一動點,若∠OPC=30°,則m的值為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com