
【題目】如圖,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 得到
得到![]() ,連接
,連接![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)如圖,![]() .
.
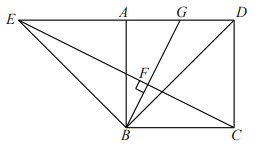
①求證:四邊形![]() 是正方形;
是正方形;
②求證:![]() 是
是![]() 中點(diǎn);
中點(diǎn);
(2)如圖,若![]() ,請(qǐng)判斷
,請(qǐng)判斷![]() 是否仍然是
是否仍然是![]() 的中點(diǎn)?若是,請(qǐng)證明;若不是,請(qǐng)說(shuō)明理由.
的中點(diǎn)?若是,請(qǐng)證明;若不是,請(qǐng)說(shuō)明理由.
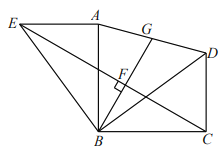
【答案】(1)①詳見(jiàn)解析;②詳見(jiàn)解析;(2)點(diǎn) ![]() 仍然是
仍然是![]() 的中點(diǎn),證明詳見(jiàn)解析.
的中點(diǎn),證明詳見(jiàn)解析.
【解析】
(1)①根據(jù)題意得出四邊形 ![]() 是平行四邊形,再由
是平行四邊形,再由![]() ,
,![]() ,得出矩形
,得出矩形![]() 是正方形.②由①得出
是正方形.②由①得出![]() ,從而得到
,從而得到![]() ,再求出
,再求出![]() ,即可解答
,即可解答
(2)延長(zhǎng)![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,延長(zhǎng)
,延長(zhǎng)![]() 交
交 ![]() 于點(diǎn)
于點(diǎn)![]() ,先求出矩形
,先求出矩形![]() 是正方形
是正方形
在證明![]() ,從而得出
,從而得出![]() ,即可解答
,即可解答
(1)證明:①![]()
![]() ,
,![]() ,
,
![]() 四邊形
四邊形 ![]() 是平行四邊形,
是平行四邊形,
![]()
![]() ,
,
![]() 平行四邊形
平行四邊形![]() 是矩形.
是矩形.
![]()
![]() ,
,
![]() 矩形
矩形![]() 是正方形.
是正方形.
②由①得![]() ,
,![]() .
.
由旋轉(zhuǎn)得![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 是
是![]() 的中點(diǎn).
的中點(diǎn).
(2)點(diǎn) ![]() 仍然是
仍然是![]() 的中點(diǎn).
的中點(diǎn).
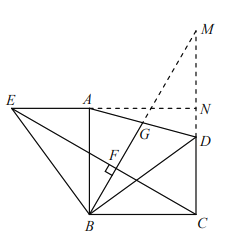
證明如下:延長(zhǎng)![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,延長(zhǎng)
,延長(zhǎng)![]() 交
交 ![]() 于點(diǎn)
于點(diǎn)![]() .
.
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() .
.
由旋轉(zhuǎn)得![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() 四邊形
四邊形![]() 是矩形.
是矩形.
![]()
![]() ,
,
![]() 矩形
矩形![]() 是正方形,
是正方形,
![]()
![]() ,
,![]() ,
,
![]()
![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
即![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 是
是![]() 中點(diǎn).
中點(diǎn).


 黎明文化寒假作業(yè)系列答案
黎明文化寒假作業(yè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
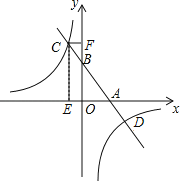
【題目】如圖,已知一次函數(shù)y=kx+b的圖象與x軸,y軸分別相交于A,B兩點(diǎn),且與反比例函數(shù)y=![]() 交于點(diǎn)C,D.作CE⊥x軸,垂足為E,CF⊥y軸,垂足為F.點(diǎn)B為OF的中點(diǎn),四邊形OECF的面積為16,點(diǎn)D的坐標(biāo)為(4,﹣b).
交于點(diǎn)C,D.作CE⊥x軸,垂足為E,CF⊥y軸,垂足為F.點(diǎn)B為OF的中點(diǎn),四邊形OECF的面積為16,點(diǎn)D的坐標(biāo)為(4,﹣b).
(1)求一次函數(shù)表達(dá)式和反比例函數(shù)表達(dá)式;
(2)求出點(diǎn)C坐標(biāo),并根據(jù)圖象直接寫(xiě)出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
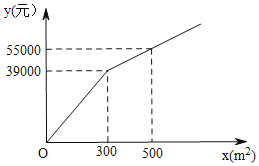
【題目】為了美化環(huán)境,建設(shè)宜居衡陽(yáng),我市準(zhǔn)備在一個(gè)廣場(chǎng)上種植甲、乙兩種花卉.經(jīng)市場(chǎng)調(diào)查,甲種花卉的種植費(fèi)用y(元)與種植面積x(m2)之間的函數(shù)關(guān)系如圖所示,乙種花卉的種植費(fèi)用為每平方米100元.
(1)求y與x的函數(shù)關(guān)系式;
(2)廣場(chǎng)上甲、乙兩種花卉的種植面積共1000m2,若甲種花卉的種植面積不少于200m2,且不超過(guò)乙種花卉種植面積的3倍,那么應(yīng)該怎忙分配甲、乙兩種花卉的種植面積才能使種植費(fèi)用最少?最少總費(fèi)用為多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】父親節(jié)即將到來(lái)之際,某商店準(zhǔn)備購(gòu)進(jìn)![]() 、
、![]() 兩種男裝進(jìn)行銷(xiāo)售,其中每套
兩種男裝進(jìn)行銷(xiāo)售,其中每套![]() 種男裝的進(jìn)價(jià)比每套
種男裝的進(jìn)價(jià)比每套![]() 種男裝的進(jìn)價(jià)多
種男裝的進(jìn)價(jià)多![]() 元用
元用![]() 元購(gòu)進(jìn)
元購(gòu)進(jìn)![]() 種男裝的數(shù)量是用
種男裝的數(shù)量是用![]() 元購(gòu)進(jìn)
元購(gòu)進(jìn)![]() 種男裝數(shù)量的
種男裝數(shù)量的![]() 倍.
倍.
(1)求每套![]() 種男裝和每套
種男裝和每套![]() 種男裝的進(jìn)價(jià)各是多少元:
種男裝的進(jìn)價(jià)各是多少元:
(2)若該商店本次購(gòu)進(jìn)![]() 種男裝的數(shù)量比購(gòu)進(jìn)
種男裝的數(shù)量比購(gòu)進(jìn)![]() 種男裝的數(shù)量的
種男裝的數(shù)量的![]() 倍還多
倍還多![]() 套,該商店每套
套,該商店每套![]() 種男裝的銷(xiāo)售價(jià)格為
種男裝的銷(xiāo)售價(jià)格為![]() 元,每套
元,每套![]() 種男裝的銷(xiāo)售價(jià)格為
種男裝的銷(xiāo)售價(jià)格為![]() 元,若將本次購(gòu)進(jìn)的
元,若將本次購(gòu)進(jìn)的![]() 、
、![]() 兩種男裝全部售出后獲得的利潤(rùn)不少于
兩種男裝全部售出后獲得的利潤(rùn)不少于![]() 元,那么該商店至少需要購(gòu)進(jìn)
元,那么該商店至少需要購(gòu)進(jìn)![]() 種男裝多少套?
種男裝多少套?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,小明想測(cè)量河對(duì)岸的一幢高樓AB的高度,小明在河邊C處測(cè)得樓頂A的仰角是60°距C處60米的E處有幢樓房,小明從該樓房中距地面20米的D處測(cè)得樓頂A的仰角是30°(點(diǎn)B.C.E在同一直線上且AB、DE均與地面BE處置),求樓AB的高________.![]()

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
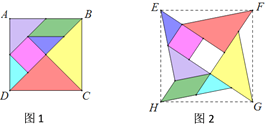
【題目】七巧板是我們祖先的一項(xiàng)卓越創(chuàng)造,被西方人譽(yù)為“東方魔板”.下面的兩幅圖正方形(如圖1)、“風(fēng)車(chē)型”(如圖2)都是由同一副七巧板拼成的,則圖中正方形ABCD,EFGH的面積比為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
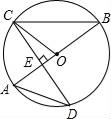
【題目】如圖,AB是圓O的直徑,CD是圓O的一條弦,且CD⊥AB于點(diǎn)E.
(1)若∠A=48°,求∠OCE的度數(shù);
(2)若CD=4![]() ,AE=2,求圓O的半徑.
,AE=2,求圓O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,BD是△ABC的角平分線,點(diǎn)E,F分別在BC,AB上,且DE∥AB,BE=AF.
(1)求證:四邊形ADEF是平行四邊形;
(2)若∠ABC=60°,BD=6,求DE的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商店購(gòu)進(jìn)一批單價(jià)為16元的日用品,銷(xiāo)售一段時(shí)間后,為了獲取更多利潤(rùn), 商店決定提高銷(xiāo)售價(jià)格,經(jīng)試驗(yàn)發(fā)現(xiàn),若按每件20元的價(jià)格銷(xiāo)售時(shí),每月能賣(mài)360件; 若按每件25元的價(jià)格銷(xiāo)售時(shí),每月能賣(mài)210件.假定每月銷(xiāo)售件數(shù)y(件)是價(jià)格x( 元/件)的一次函數(shù).
(1)試求y與x之間的函數(shù)關(guān)系式;
(2)在商品不積壓,且不考慮其他因素的條件下,問(wèn)銷(xiāo)售價(jià)格為多少時(shí),才能使每月獲得最大利潤(rùn)?每月的最大利潤(rùn)是多少?(總利潤(rùn)=總收入-總成本).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com