
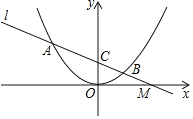
【題目】如圖,已知拋物線y=ax2過點(diǎn)A(﹣3,![]() ).
).
(1)求拋物線的解析式;
(2)已知直線l過點(diǎn)A,M(![]() ,0)且與拋物線交于另一點(diǎn)B,與y軸交于點(diǎn)C,求證:MC2=MAMB;
,0)且與拋物線交于另一點(diǎn)B,與y軸交于點(diǎn)C,求證:MC2=MAMB;
(3)若點(diǎn)P,D分別是拋物線與直線l上的動(dòng)點(diǎn),以OC為一邊且頂點(diǎn)為O,C,P,D的四邊形是平行四邊形,求所有符合條件的P點(diǎn)坐標(biāo).
【答案】(1)y=![]() x2;(2)見解析;(3)P(﹣1﹣
x2;(2)見解析;(3)P(﹣1﹣![]() ,2+
,2+![]() )或(﹣1+
)或(﹣1+![]() ,2﹣
,2﹣![]() )或(﹣2,1).
)或(﹣2,1).
【解析】
(1)利用待定系數(shù)法即可解決問題.
(2)構(gòu)建方程組確定點(diǎn)B的坐標(biāo),再利用平行線分線段成比例定理解決問題即可.
(3)如圖2中,設(shè)P(t,![]() t2),根據(jù)PD=CD構(gòu)建方程求出t即可解決問題.
t2),根據(jù)PD=CD構(gòu)建方程求出t即可解決問題.
解:(1)把點(diǎn)A(﹣3,![]() )代入y=ax2,
)代入y=ax2,
得到![]() =9a,
=9a,
∴a=![]() ,
,
∴拋物線的解析式為y=![]() x2.
x2.
(2)設(shè)直線l的解析式為y=kx+b,則有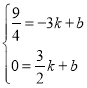 ,
,
解得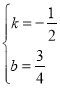 ,
,
∴直線l的解析式為y=﹣![]() x+
x+![]() ,
,
令x=0,得到y=![]() ,
,
∴C(0,![]() ),
),
由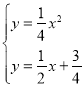 ,解得
,解得![]() 或
或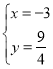 ,
,
∴B(1,![]() ),
),
如圖1中,過點(diǎn)A作AA1⊥x軸于A1,過B作BB1⊥x軸于B1,則BB1∥OC∥AA1,
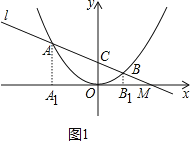
∴![]() =
=![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=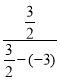 =
=![]() ,
,
∴![]() =
=![]() ,
,
即MC2=MAMB.
(3)如圖2中,設(shè)P(t,![]() t2)
t2)
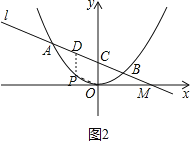
∵OC為一邊且頂點(diǎn)為O,C,P,D的四邊形是平行四邊形,
∴PD∥OC,PD=OC,
∴D(t,﹣![]() t+
t+![]() ),
),
∴|![]() t2﹣(﹣
t2﹣(﹣![]() t+
t+![]() )|=
)|=![]() ,
,
整理得:t2+2t﹣6=0或t2+2t=0,
解得t=﹣1﹣![]() 或﹣1=
或﹣1=![]() 或﹣2或0(舍棄),
或﹣2或0(舍棄),
∴P(﹣1﹣![]() ,2+
,2+![]() )或(﹣1+
)或(﹣1+![]() ,2﹣
,2﹣![]() )或(﹣2,1).
)或(﹣2,1).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在半徑為![]() 的
的![]() 中,
中,![]() 是直徑,點(diǎn)
是直徑,點(diǎn)![]() 是
是![]() 中點(diǎn),連接
中點(diǎn),連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,弦
,弦![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,過
,過![]() 的切線
的切線![]() 交
交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() ,
,![]() .
.
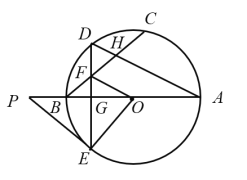
(1)求![]() 的長;
的長;
(2)連接![]() ,求證:
,求證:![]() ;
;
(3)當(dāng)點(diǎn)![]() 在
在![]() 上運(yùn)動(dòng)時(shí),連接
上運(yùn)動(dòng)時(shí),連接![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
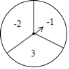
【題目】如圖,可以自由轉(zhuǎn)動(dòng)的轉(zhuǎn)盤被平均分成了三等分標(biāo)有數(shù)字﹣2,3,﹣1的扇形區(qū)域轉(zhuǎn)動(dòng)轉(zhuǎn)盤,待轉(zhuǎn)盤自動(dòng)停止后,指針指向一個(gè)扇形的內(nèi)部,則該扇形內(nèi)的數(shù)字即為轉(zhuǎn)出的數(shù)字,此時(shí),稱為轉(zhuǎn)動(dòng)轉(zhuǎn)盤一次(若指針指向兩個(gè)扇形的交線,則不計(jì)轉(zhuǎn)動(dòng)的次數(shù),重新轉(zhuǎn)動(dòng)轉(zhuǎn)盤,直到指針指向一個(gè)扇形的內(nèi)部為止)
(1)轉(zhuǎn)動(dòng)轉(zhuǎn)盤一次,求轉(zhuǎn)出的數(shù)字是3的概率;
(2)轉(zhuǎn)動(dòng)轉(zhuǎn)盤兩次,設(shè)第一次得到的數(shù)字為x,第二次得到的數(shù)字為y,點(diǎn)M的坐標(biāo)為(x,y),請用樹狀圖或列表法求點(diǎn)M在反比例函數(shù)y=﹣![]() 的圖象上的概率.
的圖象上的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某工廠準(zhǔn)備今年春季開工前美化廠區(qū),計(jì)劃對面積為![]() 的區(qū)域進(jìn)行綠化,安排甲、乙兩個(gè)工程隊(duì)完成.已知甲隊(duì)每天能完成綠化的面積是乙隊(duì)每天能完成綠化的面積的2倍,并且在獨(dú)立完成面積為
的區(qū)域進(jìn)行綠化,安排甲、乙兩個(gè)工程隊(duì)完成.已知甲隊(duì)每天能完成綠化的面積是乙隊(duì)每天能完成綠化的面積的2倍,并且在獨(dú)立完成面積為![]() 區(qū)域的綠化時(shí),甲隊(duì)比乙隊(duì)少用6天.
區(qū)域的綠化時(shí),甲隊(duì)比乙隊(duì)少用6天.
(1)求甲、乙兩工程隊(duì)每天能完成綠化的面積分別是多少![]() ?
?
(2)若工廠每天需付給甲隊(duì)的綠化費(fèi)用為0.4萬元,乙隊(duì)為0.5萬元,要使這次的綠化總費(fèi)用不超過10萬元,至少應(yīng)安排甲隊(duì)工作多少天?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】第5代移動(dòng)通信技術(shù)簡稱5G,某地已開通5G業(yè)務(wù),經(jīng)測試5G下載速度是4G下載速度的15倍,小明和小強(qiáng)分別用5G與4G下載一部600兆的公益片,小明比小強(qiáng)所用的時(shí)間快140秒,求該地4G與5G的下載速度分別是每秒多少兆?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,拋物線y = x2 – 2 m x – 2m – 2與直線y =-x-2 交于C,D兩點(diǎn),將拋物線在C、D兩點(diǎn)之間的部分(不含C、D)上恰有兩個(gè)點(diǎn)的橫坐標(biāo)為整數(shù),則m的取值范圍為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,∠ACB=90°,點(diǎn)D在BC上,BD=6,DC=2,點(diǎn)P是AB上的動(dòng)點(diǎn),則PC+PD的最小值為( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】中央電視臺(tái)的“中國詩詞大賽”節(jié)目文化品位高,內(nèi)容豐富,某校初二年級(jí)模擬開展“中國詩詞大賽”比賽,對全年級(jí)同學(xué)成績進(jìn)行統(tǒng)計(jì)后分為“優(yōu)秀”、“良好”、“一般”、“較差”四個(gè)等級(jí),并根據(jù)成績繪制成如下兩幅不完整的統(tǒng)計(jì)圖,請結(jié)合統(tǒng)計(jì)圖中的信息,回答下列問題:

(1)扇形統(tǒng)計(jì)圖中“優(yōu)秀”所對應(yīng)的扇形的圓心角為 度,并將條形統(tǒng)計(jì)圖補(bǔ)充完整.
(2)此次比賽有四名同學(xué)活動(dòng)滿分,分別是甲、乙、丙、丁,現(xiàn)從這四名同學(xué)中挑選兩名同學(xué)參加學(xué)校舉行的“中國詩詞大賽”比賽,請用列表法或畫樹狀圖法,求出選中的兩名同學(xué)恰好是甲、丁的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
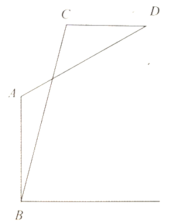
【題目】無影塔位于河南汝南城南,俗傳冬至正午無塔影,故稱無影塔;相傳為唐代和尚悟顆所建,故又稱“悟穎塔”,該塔應(yīng)建于北宋中、早期,為豫南地區(qū)現(xiàn)存最古之磚塔.某數(shù)學(xué)小組為了度量塔高進(jìn)行了如下操作:用一架無人機(jī)在距離塔基![]() 8米處垂直起飛30米至點(diǎn)
8米處垂直起飛30米至點(diǎn)![]() 處,測得塔基
處,測得塔基![]() 處的俯角為
處的俯角為![]() ,將無人機(jī)沿水平方向向右飛行
,將無人機(jī)沿水平方向向右飛行![]() 米至點(diǎn)
米至點(diǎn)![]() ,在此處測得塔頂
,在此處測得塔頂![]() 的俯角為
的俯角為![]() ,請依據(jù)題中數(shù)據(jù)計(jì)算無影塔的高度.(結(jié)果精確到
,請依據(jù)題中數(shù)據(jù)計(jì)算無影塔的高度.(結(jié)果精確到![]() ,參考數(shù)據(jù):
,參考數(shù)據(jù):![]() ,
,![]() )
)

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com