【題目】下列從左邊到右邊的變形，是因式分解的是（ ）
A.y
﹣5y﹣6＝（y﹣6）（y+1）B.a+4a﹣3＝a（a+4）﹣3
C.x（x﹣1）＝x﹣xD.m+n＝（m+n）（m﹣n）
科目：初中數學 來源： 題型：
【題目】如圖，在長方形ABCD中，AB=10厘米，BC=6厘米，點P沿AB邊從點A開始向點B以3厘米/秒的速度移動；點Q沿DA邊從點D開始向點A以2厘米/秒的速度移動.如果P、Q同時出發，用t (秒）表示移動的時間，那么：
（1）如圖1,用含t的代數式表示AP= ，AQ= .并求出當t為何值時線段AP=AQ.
（2）如圖2,在不考慮點P的情況下，連接QB，問：當t為何值時△QAB的面積等于長方形面積的
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一枚運載火箭從距雷達站C處5km的地面O處發射，當火箭到達點A，B時，在雷達站C處測得點A，B的仰角分別為34°，45°，其中點O，A，B在同一條直線上．求A，B兩點間的距離（結果精確到0.1km）．
（參考數據：sin34°=0.56，cos34°=0.83，tan34°=0.67．）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在等腰直角三角形ABC中，∠ACB=90°，AC=BC=4，D是AB的中點，E，F分別是AC，BC上的點（點E不與端點A，C重合），且AE=CF.
（1）求證：△ADE≌△CDF
（2）如圖2連接EF并取EF的中點O，連接DO并延長至點G，使GO=OD，連接DE，DF，GE，GF．求證：四邊形EDFG是正方形.
（3）當點E在什么位置時，四邊形EDFG的面積最小？直接寫出點E的位置及四邊形EDFG面積的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】自2008年實施國家知識產權戰略以來，我國具有獨立知識產權的發明專利日益增多．下圖顯示了2010﹣2013年我國發明專利申請量占世界發明專利申請量的比重．根據統計圖提供的信息，下列說法不合理的是（ ）
A. 統計圖顯示了2010﹣2013年我國發明專利申請量占世界發明專利申請量的比重的情況
B. 我國發明專利申請量占世界發明專利申請量的比重，由2010年的19.7%上升至2013年的32.1%
C. 2011年我國發明專利申請量占世界發明專利申請量的比重是28%
D. 2010﹣2013年我國發明專利申請量占世界發明專利申請量的比重逐年增長
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB＝90°，∠A＝30°，以點C為圓心，CB長為半徑作弧，交AB于點D；再分別以點B和點D為圓心，大于
的長為半徑作弧，兩弧相交于點E，作射線CE交AB于點F，若AF＝6，則BC的長為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在自習課上，小明拿來如下框的一道題目（原問題）和合作學習小組的同學們交流．
如圖1，已知△ABC，∠ACB＝90°，∠ABC＝45°，分別以AB，BC為邊向外作△ABD與△BCE，且DA＝DB，EB＝EC，∠ADB＝∠BEC＝90°，連接DE交AB于點F．探究線段DF與EF的數量關系．
小紅同學的思路是：過點D作DG⊥AB于點G，構造全等三角形，通過推理使問題得解．
小華同學說：我做過一道類似的題目，不同的是∠ABC＝30°，∠ADB＝∠BEC＝60°．
請你參考小明同學的思路，探究并解決以下問題：
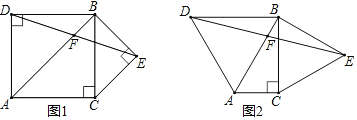
（1）寫出原問題中DF與EF的數量關系為 ．
（2）如圖2，若∠ABC＝30°，∠ADB＝∠BEC＝60°，原問題中的其他條件不變，你在（1）中得到的結論是否發生變化？請寫出你的猜想并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，
中，
，
，
，點
從
點出發沿
路徑向終點
以
的速度運動，同時點
從點出發沿
路徑向終點以
的速度運動，兩點都要到達相應的終點時才能停止運動.分別過和作
于
，
于
，則當運動時間
____________
時，
與去
全等．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
