
【題目】如圖,一塊長5米寬4米的地毯,為了美觀設計了兩橫、兩縱的配色條紋(圖中陰影部分),已知配色條紋的寬度相同,所占面積是整個地毯面積的 ![]() .
. 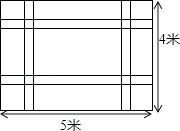
(1)求配色條紋的寬度;
(2)如果地毯配色條紋部分每平方米造價200元,其余部分每平方米造價100元,求地毯的總造價.
【答案】
(1)解:設條紋的寬度為x米.依題意得
2x×5+2x×4﹣4x2= ![]() ×5×4,
×5×4,
解得:x1= ![]() (不符合,舍去),x2=
(不符合,舍去),x2= ![]() .
.
答:配色條紋寬度為 ![]() 米
米
(2)解:條紋造價: ![]() ×5×4×200=850(元)
×5×4×200=850(元)
其余部分造價:(1﹣ ![]() )×4×5×100=1575(元)
)×4×5×100=1575(元)
∴總造價為:850+1575=2425(元)
答:地毯的總造價是2425元
【解析】考查了一元二次方程的應用,解題關鍵是要讀懂題目的意思,根據題目給出的條件,找出合適的等量關系,列出方程,再求解.注意判斷所求的解是否符合題意,舍去不合題意的解.(1)設條紋的寬度為x米,根據等量關系:配色條紋所占面積=整個地毯面積的 ![]() ,列出方程求解即可;(2)根據總價=單價×數量,可分別求出地毯配色條紋和其余部分的錢數,再相加即可求解.
,列出方程求解即可;(2)根據總價=單價×數量,可分別求出地毯配色條紋和其余部分的錢數,再相加即可求解.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的網格中,A,E為格點,B,F為小正方形邊的中點,C為AE,BF的延長線的交點.
(1)AE的長等于;
(2)若點P在線段AC上,點Q在線段BC上,且滿足AP=PQ=QB,請在如圖所示的網格中,用無刻度的直尺,畫出線段PQ,并簡要說明點P,Q的位置是如何找到的(不要求證明) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩人進行射擊訓練,兩人分別射擊12次,如圖分別統計了兩人的射擊成績,已知甲射擊成績的方差S甲2= ![]() ,平均成績
,平均成績 ![]() =8.5.
=8.5. 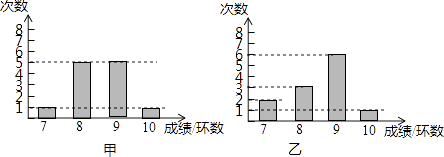
(1)根據圖上信息,估計乙射擊成績不少于9環的概率是多少?
(2)求乙射擊的平均成績的方差,并據此比較甲乙的射擊“水平”.
S2= ![]() [(x1﹣
[(x1﹣ ![]() )2+(x2﹣
)2+(x2﹣ ![]() )2…(xn﹣
)2…(xn﹣ ![]() )2].
)2].
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙二人在環形跑道上同時同地出發,同向運動.若甲的速度是乙的速度的2倍,則甲運動2周,甲、乙第一次相遇;若甲的速度是乙的速度3倍,則甲運動 ![]() 周,甲、乙第一次相遇;若甲的速度是乙的速度4倍,則甲運動
周,甲、乙第一次相遇;若甲的速度是乙的速度4倍,則甲運動 ![]() 周,甲、乙第一次相遇,…,以此探究正常走時的時鐘,時針和分針從0點(12點)同時出發,分針旋轉周,時針和分針第一次相遇.
周,甲、乙第一次相遇,…,以此探究正常走時的時鐘,時針和分針從0點(12點)同時出發,分針旋轉周,時針和分針第一次相遇.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某車間20名工人日加工零件數如表所示:
日加工零件數 | 4 | 5 | 6 | 7 | 8 |
人數 | 2 | 6 | 5 | 4 | 3 |
這些工人日加工零件數的眾數、中位數、平均數分別是( )
A.5、6、5
B.5、5、6
C.6、5、6
D.5、6、6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:

(1)試驗觀察:
如果經過兩點畫直線,那么:
第①組最多可以畫____條直線;
第②組最多可以畫____條直線;
第③組最多可以畫____條直線.
(2)探索歸納:
如果平面上有n(n≥3)個點,且任意3個點均不在1條直線上,那么經過兩點最多可以畫____條直線.(用含n的式子表示)
(3)解決問題:
某班45名同學在畢業后的一次聚會中,若每兩人握1次手問好,那么共握____次手.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣x+3與x軸、y軸分別相交于點B、C,經過B、C兩點的拋物線y=ax2+bx+c與x軸的另一個交點為A,頂點為P,且對稱軸為直線x=2.
(1)求該拋物線的解析式;
(2)連接PB、PC,求△PBC的面積;
(3)連接AC,在x軸上是否存在一點Q,使得以點P,B,Q為頂點的三角形與△ABC相似?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com