
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 邊上的動點(點
邊上的動點(點![]() 不與點
不與點![]() ,
,![]() 重合).以
重合).以![]() 為頂點作
為頂點作![]() ,射線
,射線![]() 交
交![]() 邊于點
邊于點![]() ,過點
,過點![]() 作
作![]() 交射線
交射線![]() 于點
于點![]() ,連接
,連接![]() .
.
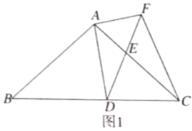
(1)求證:![]() ;
;
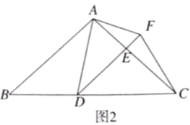
(2)當![]() 時(如圖2),求
時(如圖2),求![]() 的長;
的長;
(3)點![]() 在
在![]() 邊上運動的過程中,是否存在某個位置,使得
邊上運動的過程中,是否存在某個位置,使得![]() ?若存在,求出此時
?若存在,求出此時![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(1)詳見解析;(2)![]() ;(3)點D在BC邊上運動的過程中,存在某個位置,使得DF=CF,此時BD=9.
;(3)點D在BC邊上運動的過程中,存在某個位置,使得DF=CF,此時BD=9.
【解析】
(1)利用等腰三角形的性質有∠B=∠ACB,然后根據∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B即可得出∠BAD=∠CDE,則結論可證;
(2)過點A作AM⊥BC于M,設![]() ,在
,在![]() 中利用勾股定理求出k的值,然后利用等腰三角形三線合一求出BC的長度,然后證明△ABD∽△CBA,
中利用勾股定理求出k的值,然后利用等腰三角形三線合一求出BC的長度,然后證明△ABD∽△CBA,
則![]() ,由此可求出DB的長度,最后再利用平行線分線段成比例有
,由此可求出DB的長度,最后再利用平行線分線段成比例有![]() ,即可求出AE的長度;
,即可求出AE的長度;
(3)作FH⊥BC于H,AM⊥BC于M,AN⊥FH于N,首先證明四邊形AMHN為矩形,
則有∠MAN=90°,MH=AN,然后設![]() ,在
,在![]() 中利用勾股定理求出k的值,然后利用等腰三角形三線合一求出BC的長度,然后證明△AFN∽△ADM,
中利用勾股定理求出k的值,然后利用等腰三角形三線合一求出BC的長度,然后證明△AFN∽△ADM,
利用相似三角形的性質可求出AN的長度,進而求出CH的長度,再根據等腰三角形三線合一求出CD的長度,最后利用BD=BC-CD即可得出答案.
(1)證明:∵AB=AC,
∴∠B=∠ACB,
∵∠ADE+∠CDE=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠CDE,
∴△BAD∽△DCE.
(2)解:過點A作AM⊥BC于M.
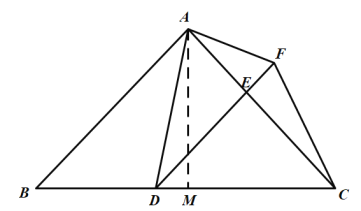
∵![]() ,
,
∴設![]() ,
,
![]()
∴![]()
解得![]() 或
或![]() (舍去)
(舍去)
∵AB=AC,AM⊥BC,
∴BC=2BM=2×4k=16,
∵DE∥AB,
∴∠BAD=∠ADE,
∵∠ADE=∠B,∠B=∠ACB,
∴∠BAD=∠ACB,
∵∠ABD=∠CBA,
∴△ABD∽△CBA,
∴![]() ,
,
∴![]()
![]() ,
,
∵DE∥AB,
∴![]() ,
,
∴![]()
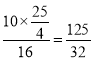 .
.
(3)點D在BC邊上運動的過程中,存在某個位置,使得DF=CF.
理由:作FH⊥BC于H,AM⊥BC于M,AN⊥FH于N.
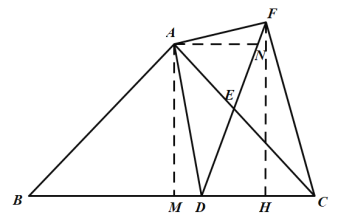
∵FH⊥BC,AM⊥BC,AN⊥FH,
∴∠NHM=∠AMH=∠ANH=90°,
∴四邊形AMHN為矩形,
∴∠MAN=90°,MH=AN,
∵AN⊥FH,AM⊥BC,
∴∠ANF=90°=∠AMD,
∵∠DAF=90°=∠MAN,
∴∠NAF=∠MAD,
∴△AFN∽△ADM,
∴![]() ,
,
∴![]() ,
,
∴CH=CM-MH=CM-AN=8-![]() =
=![]() ,
,
當DF=CF時,由點D不與點C重合,可知△DFC為等腰三角形,
∵FH⊥DC,
∴CD=2CH=7,
∴BD=BC-CD=16-7=9,
∴點D在BC邊上運動的過程中,存在某個位置,使得DF=CF,此時BD=9.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,點M、N分別在線段AC、AB上,將△ANM沿直線MN折疊,使點A的對應點D恰好落在線段BC上,當△DCM為直角三角形時,折痕MN的長為__.
+4,點M、N分別在線段AC、AB上,將△ANM沿直線MN折疊,使點A的對應點D恰好落在線段BC上,當△DCM為直角三角形時,折痕MN的長為__.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,將二次函數y=x2+2x+1的圖象沿x軸翻折,然后向右平移1個單位,再向上平移5個單位,得到二次函數y=ax2+bx+c的圖象.函數y=x2+2x+1的圖象的頂點為點A.函數y=ax2+bx+c的圖象的頂點為點C,兩函數圖象分別交于B、D兩點.
(1)求函數y=ax2+bx+c的解析式;
(2)如圖2,連接AD、CD、BC、AB,判斷四邊形ABCD的形狀,并說明理由.
(3)如圖3,連接BD,點M是y軸上的動點,在平面內是否存在一點N,使以B、D、M、N為頂點的四邊形為矩形?若存在,請求出N點的坐標;若不存在,請說明理由.
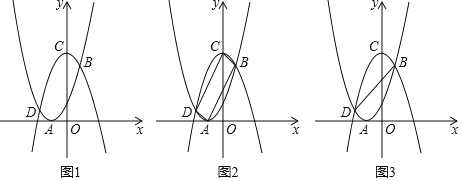
查看答案和解析>>
科目:初中數學 來源: 題型:
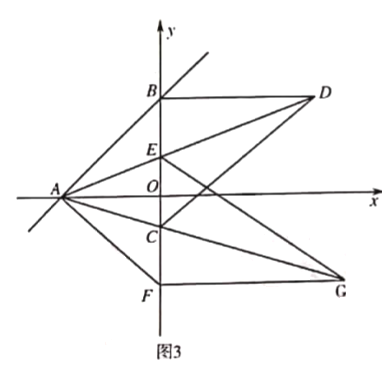
【題目】已知點![]() 是平行四邊形
是平行四邊形![]() 的邊
的邊![]() 的中點,
的中點,![]() 是對角線,
是對角線,![]() 交
交![]() 的延長線于
的延長線于![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .
.
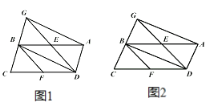
(1)如圖1,求證:![]() ;
;
(2)如圖2,當四邊形![]() 是矩形時,請你確定四邊形
是矩形時,請你確定四邊形![]() 的形狀并說明.
的形狀并說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在以“青春心向覺,建功新時代”為主題的校園文化藝術節期間,舉辦了![]() 合唱,
合唱,![]() 群舞,
群舞,![]() 書法,
書法,![]() 演講共四個項目的比賽,要求每位學生必須參加且僅參加一項,小紅隨機調查了部分學生的報名情況,并繪制了下列兩幅不完整的統計圖,請根據統計圖中信息解答下列問題:
演講共四個項目的比賽,要求每位學生必須參加且僅參加一項,小紅隨機調查了部分學生的報名情況,并繪制了下列兩幅不完整的統計圖,請根據統計圖中信息解答下列問題:
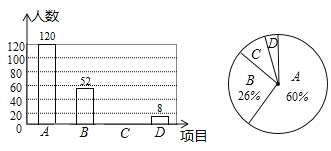
(1)本次調查的學生總人數是多少?扇形統計圖中“![]() ”部分的圓心角度數是多少?
”部分的圓心角度數是多少?
(2)請將條形統計圖補充完整;
(3)若全校共有1800名學生,請估計該校報名參加書法和演講比賽的學生共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 為坐標原點,直線
為坐標原點,直線![]() 交
交![]() 軸負半軸)軸正半軸于
軸負半軸)軸正半軸于![]() 兩點,
兩點, ![]() 的面積為4.5;
的面積為4.5;
![]() 如圖1.求
如圖1.求![]() 的值;
的值;
![]() 如圖2.在
如圖2.在![]() 軸負半軸上取點
軸負半軸上取點![]() .點
.點![]() 在第一象限,
在第一象限,![]() 連接
連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
![]() 如圖3,在
如圖3,在![]() 的條件下.
的條件下.![]() 交
交![]() 軸于點
軸于點![]() 軸交
軸交![]() 的延長線于點
的延長線于點![]() ,設
,設![]() 與
與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
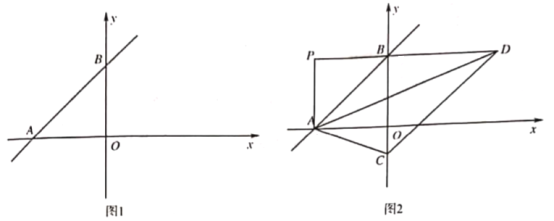
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明對九(1)、九(2)班(人數都為50人)參加“陽光體育”的情況進行了調查,統計結果如圖所示.下列說法中正確的是( )
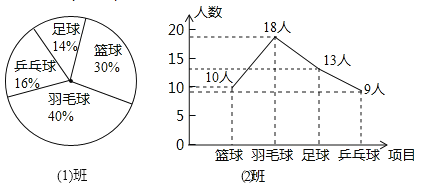
A.喜歡乒乓球的人數(1)班比(2)班多B.喜歡足球的人數(1)班比(2)班多
C.喜歡羽毛球的人數(1)班比(2)班多D.喜歡籃球的人數(2)班比(1)班多
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com