
【題目】在平面直角坐標系![]() 中,對“隔離直線”給出如下定義:點
中,對“隔離直線”給出如下定義:點![]() 是圖形
是圖形![]() 上的任意一點,點
上的任意一點,點![]() 是圖形
是圖形![]() 上的任意一點,若存在直線
上的任意一點,若存在直線![]() :
:![]() 滿足
滿足![]() 且
且![]() ,則稱直線
,則稱直線![]() :
:![]() 是圖形
是圖形![]() 與
與![]() 的“隔離直線”,如圖
的“隔離直線”,如圖![]() ,直線
,直線![]() :
:![]() 是函數(shù)
是函數(shù)![]() 的圖像與正方形
的圖像與正方形![]() 的一條“隔離直線”.
的一條“隔離直線”.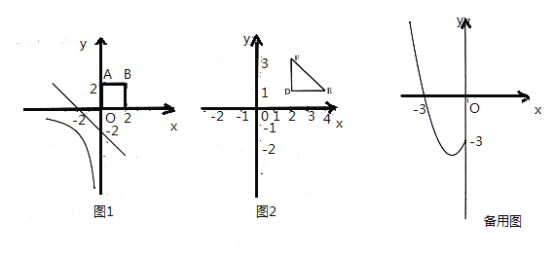
(1)在直線①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是圖
中,是圖![]() 函數(shù)
函數(shù)![]() 的圖像與正方形
的圖像與正方形![]() 的“隔離直線”的為 .
的“隔離直線”的為 .
(2)如圖![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的兩腰分別與坐標軸平行,直角頂點
的兩腰分別與坐標軸平行,直角頂點![]() 的坐標是
的坐標是![]() ,⊙O的半徑為
,⊙O的半徑為![]() ,是否存在
,是否存在![]() 與⊙O的“隔離直線”?若存在,求出此“隔離直線”的表達式:若不存在,請說明理由;
與⊙O的“隔離直線”?若存在,求出此“隔離直線”的表達式:若不存在,請說明理由;
(3)正方形![]() 的一邊在
的一邊在![]() 軸上,其它三邊都在
軸上,其它三邊都在![]() 軸的左側(cè),點
軸的左側(cè),點![]() 是此正方形的中心,若存在直線
是此正方形的中心,若存在直線![]() 是函數(shù)
是函數(shù)![]() 的圖像與正方形
的圖像與正方形![]() 的“隔離直線”,請直接寫出
的“隔離直線”,請直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)①④;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根據(jù)的“隔離直線”的定義即可解決問題;
(2)存在,連接![]() ,求得
,求得![]() 與
與![]() 垂直且過
垂直且過![]() 的直接就是“隔離直線”,據(jù)此即可求解;
的直接就是“隔離直線”,據(jù)此即可求解;
(3)分兩種情形正方形在x軸上方以及在x軸下方時,分別求出正方形的一個頂點在直線![]() 上時的t的值即可解決問題.
上時的t的值即可解決問題.
(1)根據(jù)的“隔離直線”的定義可知![]() ,是圖1函數(shù)
,是圖1函數(shù)![]() 的圖象與正方形OABC的“隔離直線”;直線
的圖象與正方形OABC的“隔離直線”;直線![]() 也是圖1函數(shù)
也是圖1函數(shù)![]() 的圖象與正方形OABC的“隔離直線”;而
的圖象與正方形OABC的“隔離直線”;而![]() 與
與![]() 不滿足圖1函數(shù)
不滿足圖1函數(shù)![]() 的圖象與正方形OABC的“隔離直線”的條件;
的圖象與正方形OABC的“隔離直線”的條件;
故答案為:①④;
(2)存在,
理由如下:
連接![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,如圖,
,如圖,
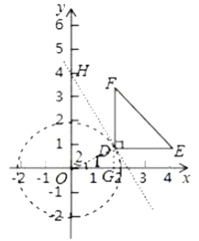
在Rt△DGO中,![]() ,
,
∵⊙O的半徑為![]() ,
,
∴點D在⊙O上.
過點D作DH⊥OD交y軸于點H,
∴直線DH是⊙O的切線,也是△EDF與⊙O的“隔離直線”.
設(shè)直線OD的解析式為![]() ,
,
將點D(2,1)的坐標代入得![]() ,
,
解得:![]() ,
,
∵DH⊥OD,
∴設(shè)直線DH的解析式為![]() ,
,
將點D(2,1)的坐標代入得![]() ,
,
解得:![]() ,
,
∴直線DH的解析式為![]() ,
,
∴“隔離直線”的表達式為![]() ;
;
(3)如圖:
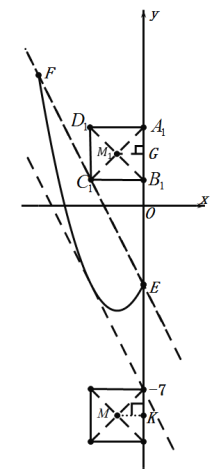
由題意點F的坐標為(![]() ),
),
當直線![]() 經(jīng)過點F時,
經(jīng)過點F時,![]() ,
,
∴![]() ,
,
∴直線![]() ,即圖中直線EF,
,即圖中直線EF,
∵正方形A1B1C1D1的中心M(1,t),
過點![]() 作
作![]() ⊥y軸于點G,
⊥y軸于點G,
∵點![]() 是正方形的中心,且
是正方形的中心,且![]() ,
,
∴B1C1![]() ,
,![]() ,
,
∴正方形A1B1C1D1的邊長為2,
當![]() 時,
時,![]() ,
,
∴點C1的坐標是(![]() ),此時直線EF是函數(shù)
),此時直線EF是函數(shù)![]() )的圖象與正方形A1B1C1D1的“隔離直線”,
)的圖象與正方形A1B1C1D1的“隔離直線”,
∴點![]() 的坐標是(-1,2),
的坐標是(-1,2),
此時![]() ;
;
當直線![]() 與
與![]() 只有一個交點時,
只有一個交點時,
![]() ,消去y得到
,消去y得到![]() ,
,
由![]() ,可得
,可得![]() ,
,
解得:![]() ,
,
同理,此時點M的坐標為:(![]() ),
),
∴![]() ,
,
根據(jù)圖象可知:
當![]() 或
或![]() 時,直線
時,直線![]() 是函數(shù)
是函數(shù)![]() )的圖象與正方形A1B1C1D1的“隔離直線”.
)的圖象與正方形A1B1C1D1的“隔離直線”.


科目:初中數(shù)學 來源: 題型:
【題目】![]() 內(nèi)接于
內(nèi)接于![]() 邊于點
邊于點![]() ,連接
,連接![]() .
.
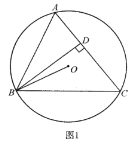
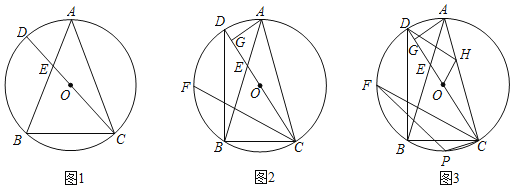
![]() 如圖1,求證:
如圖1,求證:![]() ;
;
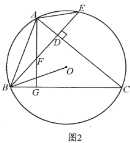
![]() 如圖2,延長
如圖2,延長![]() 交
交![]() 于點
于點![]() ,點
,點![]() 在線段
在線段![]() 上,射線
上,射線![]() 交
交![]() 邊于點
邊于點![]() ,連接
,連接![]() ,若
,若![]() ,求證:
,求證:![]() ;
;
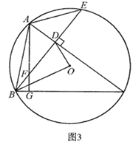
![]() 如圖3,在
如圖3,在![]() 的條件下,連接
的條件下,連接![]() ,若
,若![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為4,∠DAC的平分線交DC于點E,若點P,Q分別是AD和AE上的動點,則DQ+PQ的最小值是________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
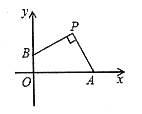
【題目】如圖,點![]() 的坐標為
的坐標為![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() 軸,
軸,![]() 軸的正半軸上運動,且
軸的正半軸上運動,且![]() ,下列結(jié)論:
,下列結(jié)論:
①![]()
②當![]() 時四邊形
時四邊形![]() 是正方形
是正方形
③四邊形![]() 的面積和周長都是定值
的面積和周長都是定值
④連接![]() ,
,![]() ,則
,則![]() ,其中正確的有( )
,其中正確的有( )
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D點,O是AB上一點,經(jīng)過A、D兩點的⊙O分別交AB、AC于點E、F.
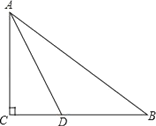
(1)用尺規(guī)補全圖形(保留作圖痕跡,不寫作法);
(2)求證:BC與⊙O相切;
(3)當AD=2![]() ,∠CAD=30°時,求劣弧AD的長.
,∠CAD=30°時,求劣弧AD的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知拋物線y=-x2+mx+3與x軸交于點A、B兩點,與y軸交于C點,點B的坐標為(3,0),拋物線與直線y=-![]() x+3交于C、D兩點.連接BD、AD.
x+3交于C、D兩點.連接BD、AD.

(1)求m的值.
(2)拋物線上有一點P,滿足S△ABP=4S△ABD,求點P的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:![]() 內(nèi)接于⊙
內(nèi)接于⊙![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,交⊙
,交⊙![]() 于點
于點![]() ,滿足
,滿足![]() .
.
(1)如圖1,求證:![]() ;
;
(2)如圖2,連接![]() ,點
,點![]() 為弧
為弧![]() 上一點,連接
上一點,連接![]() ,
,![]() =
=![]() ,過點
,過點![]() 作
作![]() ,垂足為點
,垂足為點![]() ,求證:
,求證:![]() ;
;
(3)如圖3,在(2)的條件下,點![]() 為
為![]() 上一點,分別連接
上一點,分別連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,交⊙
,交⊙![]() 于點
于點![]() ,
,![]() ,
,![]() ,連接
,連接![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】隨著信息技術(shù)的迅猛發(fā)展,人們?nèi)ド虉鲑徫锏闹Ц斗绞礁佣鄻印⒈憬荩谝淮钨徫镏校瑥埲A和李紅都想從“微信”、“支付寶”、“銀行卡”、“現(xiàn)金”四種支付方式中選一種方式進行支付.
(1)張華用“微信”支付的概率是______.
(2)請用畫樹狀圖或列表法求出兩人恰好選擇同一種支付方式的概率.(其中“微信”、“支付寶”、“銀行卡”、“現(xiàn)金”分別用字母“A”“B”“C”“D”代替)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com