
【題目】已知點E、F分別是四邊形ABCD邊AB、AD上的點,且DE與CF相交于點G.
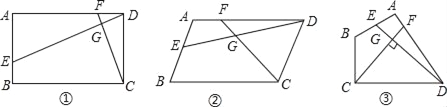
(1)如圖①,若AB∥CD,AB=CD,∠A=90°,且ADDF=AEDC,求證:DE⊥CF:
(2)如圖②,若AB∥CD,AB=CD,且∠A=∠EGC時,求證:DECD=CFDA:
(3)如圖③,若BA=BC=3,DA=DC=4,設DE⊥CF,當∠BAD=90°時,試判斷![]() 是否為定值,并證明.
是否為定值,并證明.
【答案】(1)證明見解析 (2)證明見解析 (3)答案見解析
【解析】
(1)根據已知條件得到四邊形ABCD是矩形,由矩形的性質得到∠A=∠FDC=90°,根據相似三角形的性質得到∠CFD=∠AED,根據余角的性質即可得到結論;
(2)根據已知條件得到△DFG∽△DEA,推出![]() ,根據△CGD∽△CDF,得到
,根據△CGD∽△CDF,得到
![]() ,等量代換即可得到結論;
,等量代換即可得到結論;
(3)過C作CN⊥AD于N,CM⊥AB交AB延長線于M,連接BD,設CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,證△BCM∽△DCN,求出![]() ,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,解方程得到CN,證出△AED∽△NFC,即可得出答案.
,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,解方程得到CN,證出△AED∽△NFC,即可得出答案.
(1)證明:∵AB∥CD,AB=CD,∠A=90°,
∴四邊形ABCD是矩形,
∴∠A=∠FDC=90°,
∵ADDF=AEDC,
∴![]()
∴△AED∽△DFC,
∴∠CFD=∠AED,
∵∠ADE+∠AED=90°,
∴∠ADE+∠CFD=90°,
∴∠DGF=90°,
∴DE⊥CF;
(2)證明:∵∠A=∠EGC,∠ADE=∠GDF,
∴△DFG∽△DEA,
∴![]()
∵AB∥CD,AB=CD,
∴四邊形ABCD是平行四邊形,∠AED=∠EDC,
∴∠B=∠ADC,
∵△DFG∽△DEA,
∴∠AED=∠DFG,
∴DFC=∠GDC,
∵∠DCG=∠FCD,
∴△CGD∽△CDF,
∴![]()
∴![]() ,
,
∴DECD=CFDA;
(3)解:![]() 為定值,
為定值,
理由:過C作CN⊥AD于N,CM⊥AB交AB延長線于M,連接BD,設CN=x,
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四邊形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中,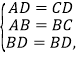
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴![]() ,
,
∴![]()
∴![]()
在Rt△CMB中,![]() ,BM=AM﹣AB=x﹣3,由勾股定理得:BM2+CM2=BC2,
,BM=AM﹣AB=x﹣3,由勾股定理得:BM2+CM2=BC2,
∴![]()
x=0(舍去),![]()
∴![]()
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴![]()


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:初中數學 來源: 題型:
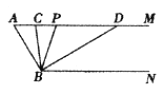
【題目】如圖,已知AM//BN,∠A=600.點P是射線AM上一動點(與點A不重合),BC、BD分別平分∠ABP和∠PBN,分別交射線AM于點C,D.
(1)①∠ABN的度數是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度數;
(3)當點P運動時,∠APB與∠ADB之間的數量關系是否隨之發生變化?若不變化,請寫出它們之間的關系,并說明理由;若變化,請寫出變化規律.
(4)當點P運動到使∠ACB=∠ABD時,∠ABC的度數是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知線段AB=12,點M、N是線段AB上的兩點,且AM=BN=2,點P是線段MN上的動點,分別以線段AP、BP為邊在AB的同側作正方形APDC、正方形PBFE,點G、H分別是CD、EF的中點,點O是GH的中點,當P點從M點到N點運動過程中,OM+OB的最小值是( )

A.10B.12C.2 ![]() D.12
D.12![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算題:
(1)(-20)+(+3)+(-5)+(+7);
(2)16-(-15)-4+(-5);
(3)(-12)×(-37)×![]() ;
;
(4)(-![]() )÷
)÷![]() ÷(-
÷(-![]() );
);
(5)-30×(![]()
![]()
![]() );
);
(6)-3-[-5 +(1-![]() ×0.6)÷(-3)]
×0.6)÷(-3)]
(7)![]()
(8)![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
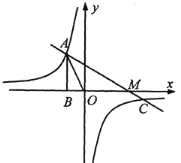
【題目】如圖,已知反比例函數 y=![]() 的圖像經過點A(-1,a),過點A作AB⊥x軸,垂足為點B,△AOB的面積為
的圖像經過點A(-1,a),過點A作AB⊥x軸,垂足為點B,△AOB的面積為![]() .
.
(1)求a、k的值;
(2)若一次函數y=mx+n圖像經過點A和反比例函數圖像上另一點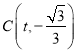 ,且與x軸交于M點,求AM的值:
,且與x軸交于M點,求AM的值:
(3)在(2)的條件下,如果以線段AM為一邊作等邊△AMN,頂點N在一次數函數y=bx上,則b= ______.
查看答案和解析>>
科目:初中數學 來源: 題型:
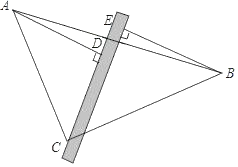
【題目】將含有45°角的直角三角板ABC和直尺如圖擺放在桌子上,然后分別過A、B兩個頂點向直尺作兩條垂線段AD,BE.
(1)請寫出圖中的一對全等三角形并證明;
(2)你能發現并證明線段AD,BE,DE之間的關系嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場用14500元購進甲、乙兩種礦泉水共500箱,礦泉水的成本價與銷售價如表(二)所示:
類別 | 成本價(元/箱) | 銷售價(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)購進甲、乙兩種礦泉水各多少箱?
(2)該商場售完這500箱礦泉水,可獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
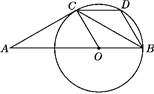
【題目】如圖,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一點O,使OB=OC,以點O為圓心,OB為半徑作圓,過點C作CD∥AB交⊙O于點D,連接BD.
(1)猜想AC與⊙O的位置關系,并證明你的猜想;
(2)試判斷四邊形BOCD的形狀,并證明你的判斷;
(3)已知AC=6,求扇形OBC所圍成的圓錐的底面圓的半徑r.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com