
【題目】已知:如圖,在![]() 中,
中,![]() ,
,![]() ,垂足為點
,垂足為點![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分線,
的平分線,![]() ,垂足為點
,垂足為點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .
.

![]() 求證:四邊形
求證:四邊形![]() 為矩形;
為矩形;
![]() 當
當![]() 滿足什么條件時,四邊形
滿足什么條件時,四邊形![]() 是一個正方形?并給出證明.
是一個正方形?并給出證明.
![]() 在
在![]() 的條件下,若
的條件下,若![]() ,求正方形
,求正方形![]() 周長.
周長.
【答案】![]() 證明見解析;(2)
證明見解析;(2)![]() 且
且![]() 時,四邊形
時,四邊形![]() 是一個正方形;(3)8.
是一個正方形;(3)8.
【解析】
(1)根據已知條件證明∠DAE=90°,已知CE⊥AN,AD⊥BC,根據有三個角是直角的四邊形是矩形,可以證明四邊形ADCE為矩形;(2)![]() 且
且![]() 時,四邊形
時,四邊形![]() 是一個正方形,根據添加的條件證明
是一個正方形,根據添加的條件證明![]() ,即可判定四邊形ADCE為正方形;(3)根據勾股定理求得AD的長,根據正方形的性質即可求得正方形ADCE周長.
,即可判定四邊形ADCE為正方形;(3)根據勾股定理求得AD的長,根據正方形的性質即可求得正方形ADCE周長.
![]() 證明:∵
證明:∵![]() ,
,![]() ,垂足為點
,垂足為點![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 外角
外角![]() 的平分線,
的平分線,
∴![]() .
.
∵![]() 與
與![]() 是鄰補角,
是鄰補角,
∴![]() ,
,
∴![]() .
.
即∠DAE=90°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四邊形![]() 為矩形;
為矩形;
![]() 且
且![]() 時,四邊形
時,四邊形![]() 是一個正方形,
是一個正方形,
證明:∵![]() 且
且![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵四邊形![]() 為矩形,
為矩形,
∴四邊形![]() 為正方形;
為正方形;
![]() 由勾股定理,得
由勾股定理,得
![]() ,
,![]() ,
,
即![]() ,
,
![]() ,
,
正方形![]() 周長
周長![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=30°,邊AB的垂直平分線DE交AB于點E,交BC于點D.CD=3,則BC的長為( )

A. 6 B. 9 C. 6![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AM,CN分別是∠BAD和∠BCD的平分線,添加一個條件,仍無法判斷四邊形AMCN為菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分線 D.∠BAD=120°
查看答案和解析>>
科目:初中數學 來源: 題型:
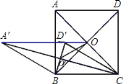
【題目】如圖,邊長為![]() 的正方形
的正方形![]() 的對角線交于點
的對角線交于點![]() ,把邊
,把邊![]() 、
、![]() 分別繞點
分別繞點![]() 、
、![]() 同時逆時針旋轉
同時逆時針旋轉![]() 得四邊形
得四邊形![]() ,其對角線交點為
,其對角線交點為![]() ,連接
,連接![]() .下列結論:
.下列結論:
①四邊形![]() 為菱形;
為菱形;
②![]() ;
;
③線段![]() 的長為
的長為![]() ;
;
④點![]() 運動到點
運動到點![]() 的路徑是線段
的路徑是線段![]() .其中正確的結論共有( )
.其中正確的結論共有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正比例函數y=2x的圖象與一次函數y=kx+b的圖象交于點A(m,2),一次函數的圖象經過點B(2,1).
(1)求一次函數的解析式;
(2)請直接寫出不等式組1<kx +b<2x的解集。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com