
【題目】溫州蒼南馬站四季柚,聲名遠播,今年又是一個豐收年,某經銷商為了打開銷路,對1 000個四季柚進行打包優惠出售.打包方式及售價如圖所示.假設用這兩種打包方式恰好裝完全部柚子.
(1)若銷售a箱紙盒裝和a袋編織袋裝四季柚的收入共950元,求a的值;
(2)當銷售總收入為7 280元時:
①若這批四季柚全部售完,請問紙盒裝共包裝了多少箱,編織袋裝共包裝了多少袋.
②若該經銷商留下b(b>0)箱紙盒裝送人,其余柚子全部售出,求b的值.

【答案】(1) a=5;(2)①紙盒裝共包裝了35箱,編織袋裝共包裝了40袋;②b為9.
【解析】
(1)根據收入共950元,可得出一元一次方程,解出即可;
(2)①紙盒裝共包裝了x箱,則編織袋裝共包裝y 袋,根據等量關系可得出方程組,解出即可;②根據①的關系可以y表示出x,減去留下的b箱紙盒裝,再由銷售總收入為7280元,可得出方程,解出即可.
(1)由題意得64a+126a=950,得a=5.
(2)①設紙盒裝共包裝了x箱,編織袋裝共包裝了y袋.
由題意得![]()
解得![]()
∴紙盒裝共包裝了35箱,編織袋裝共包裝了40袋.
②當8x+18y=1 000時,得x=![]() =125-
=125-![]() ,由題意得64
,由題意得64![]() +126y=7 280,得y=40-
+126y=7 280,得y=40-![]() .
.
∵x,y,b都為整數,且x≥0,y≥0,b>0,
∴b=9,x=107,y=8.∴b為9.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】十八世紀瑞士數學家歐拉證明了簡單多面體中頂點數(V)、面數(F)、棱數(E)之間存在的一個有趣的關系式,請你觀察下列幾種簡單多面體模型,解答下列問題:

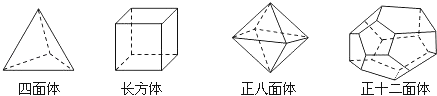
圖1 圖2
(探索新知)如圖1,(1)根據上面多面體模型,完成表格中的空格;
多面體 | 頂點數(V) | 面數(F) | 棱數(E) |
四面體 | 4 | 4 | |
長方體 | 8 | 6 | 12 |
正八面體 | 8 | 12 | |
正十二面體 | 20 | 12 | 30 |
你發現頂點數(V)、面數(F)、棱數(E)之間存在的關系式是 .
(2)根據以上關系式猜想是否存在一個多面體,它有16個面,50條棱,34個頂點?并寫出理由。
(實際應用)如圖2,足球一般有32塊黑白皮子縫合而成,黑色的是正五邊形,白色的是正六邊形,如
果我們近似把足球看成一個多面體.
(1)設黑色的正五邊形有x塊,則白色的正六邊形有(32﹣x)塊,當把足球看成一個多面體時,它的棱數是 ,它的頂點數是 .
(2)求出黑皮和白皮各有多少塊?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AE上一動點(不與點A,E重合),在AE同側分別作等邊△ABC和等邊△CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ.以下五個結論:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正確的結論的個數是( )
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分線,點E,F分別是邊AC, BC上的動點,AC=4,設AE=x,BF=y.
(1)若x+y=3,求四邊形CEDF的面積;
(2)當DE⊥DF時,如圖2,試探索x、y之間的數量關系.
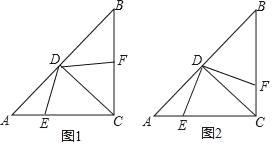
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B、C 為數軸上三點,若點 C 到點 A 的距離是點 C 到點 B 的距離的 2倍,則稱點 C 是(A,B)的奇異點,例如圖 1 中,點 A 表示的數為﹣1,點B 表示的數為 2,表示 1 的點 C 到點 A 的距離為 2,到點 B 的距離為 1,則點C 是(A,B)的奇異點,但不是(B,A)的奇異點.
(1)在圖 1 中,直接說出點 D 是(A,B)還是(B,C)的奇異點;
(2)如圖 2,若數軸上 M、N 兩點表示的數分別為﹣2 和 4,(M,N)的奇異點 K 在 M、N 兩點之間,請求出 K 點表示的數;
(3)如圖 3,A、B 在數軸上表示的數分別為﹣20 和 40,現有一點 P 從點 B 出發,向左運動.
①若點 P 到達點 A 停止,則當點 P 表示的數為多少時,P、A、B 中恰有一個點為其余兩點的奇異點?
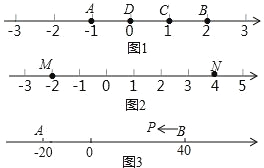
②若點 P 到達點 A 后繼續向左運動,是否存在使得 P、A、B 中恰有一個點為其余兩點的奇異點的情況?若存在,請直接寫出此時 PB 的距離;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列解題過程:(-15)÷(![]() -3)×6
-3)×6
(解析)原式=(-15)÷(-![]() )×6 (第一步)
)×6 (第一步)
=(-15)÷(-25)(第二步)
=-![]() (第三步)
(第三步)
解答問題:
①上面解答過程有兩個錯誤,第一處是第______步,錯誤的原因是______;第二處是第______步,錯誤的原因是______;
②請你正確解答本題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=(m+2)x+3-n,
(l)m,n是何值時,y隨x的增大而減小?
(2)m,n為何值時,函數的圖象經過原點?
(3)若函數圖象經過第二、三、四象限,求 m,n的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com