
【題目】關于![]() 的一元二次方程
的一元二次方程![]() 有兩個不相等且非零的實數(shù)根,探究
有兩個不相等且非零的實數(shù)根,探究![]() 滿足的條件.
滿足的條件.
小華根據(jù)學習函數(shù)的經(jīng)驗,認為可以從二次函數(shù)的角度研究一元二次方程的根的符號。下面是小華的探究過程:第一步:設一元二次方程![]() 對應的二次函數(shù)為
對應的二次函數(shù)為![]() ;
;
第二步:借助二次函數(shù)圖象,可以得到相應的一元二次方程中![]() 滿足的條件,列表如下表。
滿足的條件,列表如下表。
方程兩根的情況 | 對應的二次函數(shù)的大致圖象 |
|
方程有兩個不相等的負實根 |
|
|
①_______ |
|
|
方程有兩個不相等的正實根 | ② | ③____________ |
(1)請將表格中①②③補充完整;
(2)已知關于![]() 的方程
的方程![]() ,若方程的兩根都是正數(shù),求
,若方程的兩根都是正數(shù),求![]() 的取值范圍.
的取值范圍.
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是邊
是邊![]() 上一個動點(不與
上一個動點(不與![]() 、
、![]() 重合),點
重合),點![]() 為射線
為射線![]() 上一點,且
上一點,且![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 為半徑作
為半徑作![]() ,設
,設![]() .
.
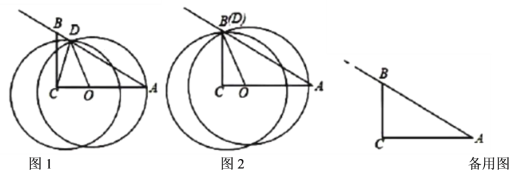
(1)如圖2,當點![]() 與點
與點![]() 重合時,求
重合時,求![]() 的值;
的值;
(2)當點![]() 在線段
在線段![]() 上,如果
上,如果![]() 與
與![]() 的另一個交點
的另一個交點![]() 在線段
在線段![]() 上時,設
上時,設![]() ,試求
,試求![]() 與
與![]() 之間的函數(shù)解析式,并寫出
之間的函數(shù)解析式,并寫出![]() 的取值范圍;
的取值范圍;
(3)在點![]() 的運動過程中,如果
的運動過程中,如果![]() 與線段
與線段![]() 只有一個公共點,請直接寫出
只有一個公共點,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我省某工廠為全運會設計了一款成本每件20元的工藝品,投放市場試銷后發(fā)現(xiàn)銷售量y(件)是售價x(元/件)的一次函數(shù),當售價為23元/件時,每天銷售量為790件;當售價為25元/件,每天銷售量為750件.
(1)求y與x的函數(shù)關系;
(2)如果該工藝品最高不超過每件30元,那么售價定位每件多少元時,工藝廠銷售該工藝品每天獲得的利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,![]() 的半徑為
的半徑為![]() ,
,![]() 是
是![]() 的直徑,
的直徑,![]() 是
是![]() 上一點,連接
上一點,連接![]() 、
、![]() .
.![]() 為劣弧
為劣弧![]() 的中點,過點
的中點,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,![]() ,交
,交![]() 的延長線于點
的延長線于點![]() .
.

(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)連接![]() ,若
,若![]() ,如圖2.
,如圖2.
①求![]() 的長;
的長;
②圖中陰影部分的面積等于_________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,點C將線段AB分成兩部分,若AC2=BCAB(AC>BC),則稱點C為線段AB的黃金分割點.某數(shù)學興趣小組在進行拋物線課題研究時,由黃金分割點聯(lián)想到“黃金拋物線”,類似地給出“黃金拋物線”的定義:若拋物線y=ax2+bx+c,滿足b2=ac(b≠0),則稱此拋物線為黃金拋物線.
(Ⅰ)若某黃金拋物線的對稱軸是直線x=2,且與y軸交于點(0,8),求y的最小值;
(Ⅱ)若黃金拋物線y=ax2+bx+c(a>0)的頂點P為(1,3),把它向下平移后與x軸交于A(![]() +3,0),B(x0,0),判斷原點是否是線段AB的黃金分割點,并說明理由.
+3,0),B(x0,0),判斷原點是否是線段AB的黃金分割點,并說明理由.
![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
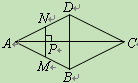
【題目】如圖,點P是菱形ABCD的對角線AC上的一個動點,過點P垂直于AC的直
線交菱形ABCD的邊于M、N兩點.設AC=2,BD=1,AP=x,△AMN的面積為y,則
y關于x的函數(shù)圖象大致形狀是【 】

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖是拋物線![]() 的部分圖象,其頂點為
的部分圖象,其頂點為![]() ,與
,與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸的一個交點為
軸的一個交點為![]() ,連接
,連接![]() .以下結論:①
.以下結論:①![]() ;②拋物線經(jīng)過點
;②拋物線經(jīng)過點![]() ;③
;③![]() ;④當
;④當![]() 時,
時, ![]() .其中正確的是( )
.其中正確的是( )
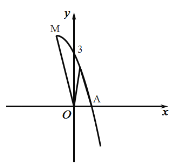
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】4月23日,為迎接“世界讀書日”,某書城開展購書有獎活動.顧客每購書滿100元獲得一次摸獎機會,規(guī)則為:一個不透明的袋子中裝有4個小球,小球上分別標有數(shù)字1,2,3,4,它們除所標數(shù)字外完全相同,搖勻后同時從中隨機摸出兩個小球,則兩球所標數(shù)字之和與獎勵的購書券金額的對應關系如下:
兩球所標數(shù)字之和 | 3 | 4 | 5 | 6 | 7 |
獎勵的購書券金額(元) | 0 | 0 | 30 | 60 | 90 |
(1)通過列表或畫樹狀圖的方法計算摸獎一次獲得90元購書券的概率;
(2)書城規(guī)定:如果顧客不愿意參加摸獎,那么可以直接獲得30元的購書券.在“參加摸獎”和“直接獲得購書券”兩種方式中,你認為哪種方式對顧客更合算?請通過求平均教的方法說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,AB=6,BC=4,點E在邊AB上(不與點A、B重合),過點D作DF⊥DE,交邊BC的延長線于點F.
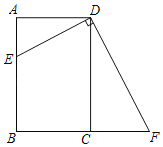
(1)求證:△DAE∽△DCF.
(2)設線段AE的長為x,線段BF的長為y,求y與x之間的函數(shù)關系式.
(3)當四邊形EBFD為軸對稱圖形時,則cos∠AED的值為 .
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com